| 기본 개념 | 여러 방식 비교 | 6 Step, SPWM, SVPWM 등 비교 | https://bahk33.tistory.com/230 | |
| PWM 에 대하여 | https://bahk33.tistory.com/215 | |||
| DQ 변환 | 본글 https://bahk33.tistory.com/218 | |||
| 스칼라와 벡터 비교 | https://bahk33.tistory.com/229 | |||
| 스칼라 | VF ( V/f, VVVF ) 인코더 사용 안함. |
Square Wave Inverter, Six Step Inverter |
VF,VVVF https://bahk33.tistory.com/216 | |
| SPWM, Sinusoidal PWM | SPWM https://bahk33.tistory.com/217 | |||
| 슬립 주파수 제어 SFC, Slip Freq Control 인코더 사용 |
||||
| DTC Direct Torque Control 스위칭 기반 |
SVM, SVPWM, Space Vector PWM | SVPWM https://bahk33.tistory.com/219 소스 https://bahk33.tistory.com/231 |
||
| PTC, MPC 기반 DTC | ||||
| 벡터 | FOC Field-Oriented Control |
DFOC, 직접 벡터 제어 |
센서 , 인코더 사용 | |
| 센서리스, 인코더 사용 안함 |
||||
| IFOC 간접 벡터 제어 |
센서 | |||
| 센서리스 | ||||
============================
목차
1. DQ ( Direct Quadrature ) 변환
2. 클라크 변환
3. Clarke 변환 행렬 유도
4. 개별 벡터 구하기
=====================
1. DQ ( Direct Quadrature ) 변환
> DQ변환은, 3상 회로분석을 간단히 하기 위한 변환으로,
2가지 변환 즉 Clarke 변환과 Park 변환의 곱을 말한다.
> 먼저 Clarke 변환( 또는 αβ 변환) 은 3상의 교류 파형을 2상의 교류 파형으로 바꾸는 거로 Edith Clake가 1937년과 1938년 논문 발표 하였읍니다.
> 두번째로 park변환은 정지 좌표계를 회전 좌표계로 바꾸는,
즉 2상 교류 파형을 2상 직류 파형으로 바꾸는 것으로 Robert H. Park 가 1929년 논문 발표 하였읍니다.
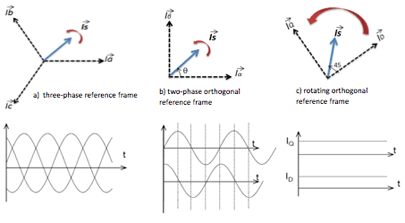
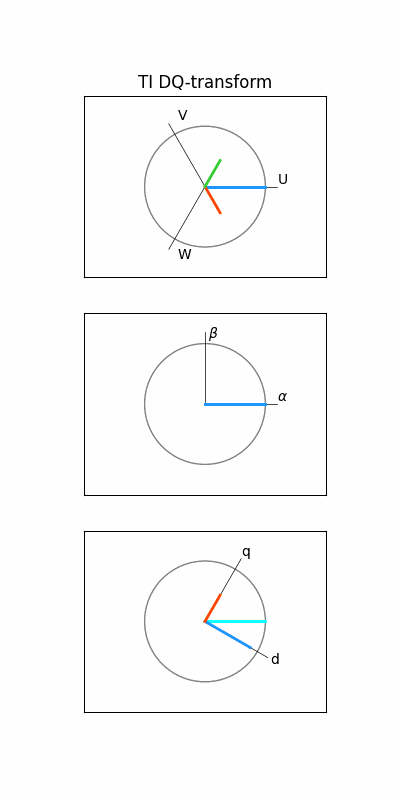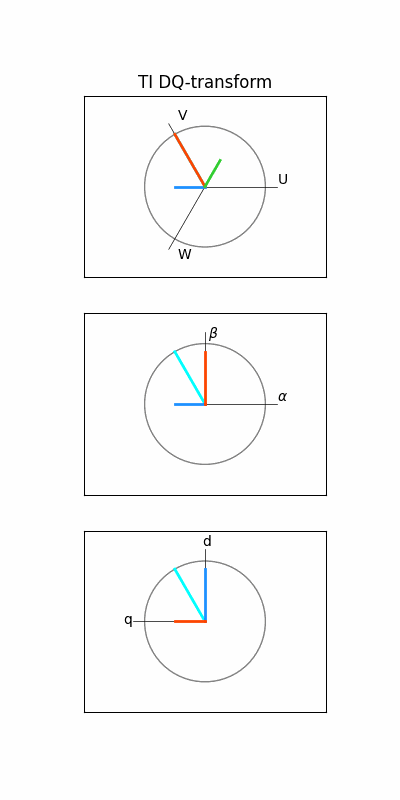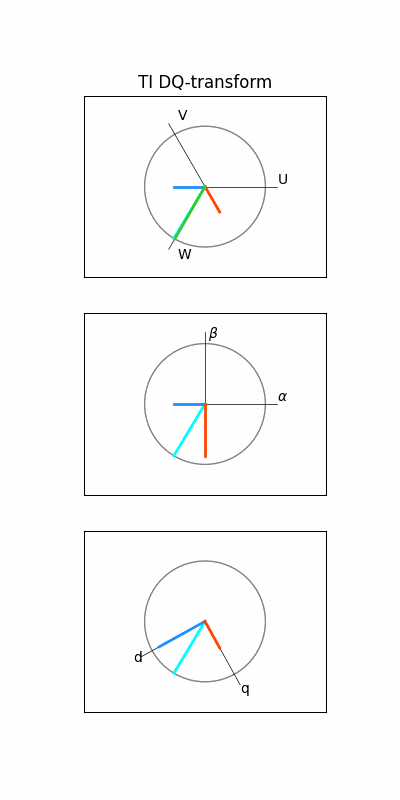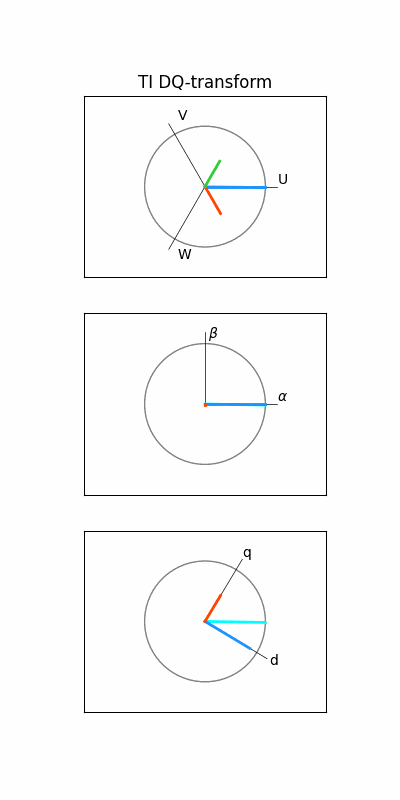
> 두 변환을 거치면, 아래 그림과 같이
3상의 교류 파형 -> 2상의 교류 파형 -> 2상 직류 파형
이 됩니다.

> dq 역변환은 Park 역변환 후 Clarke 역변환하는 것입니다.
> 3상 교류모터를 돌기기 위한 PWM 방식에서
- SVPWM(Space Vector) 은 dq변환을 이용 하고,
- 벡터 제어(또는 FOC, Field-Oriented Control)방식은 dq변환, dq역변환을 이용 합니다.
FOC는 1970년대 처음 나오고, 1980년대에 상용화 되었읍니다.
클락 변환과 파크 변환을 통해 얻어진 직교 좌표계의 벡터 다이어그램은 아래와 같습니다.
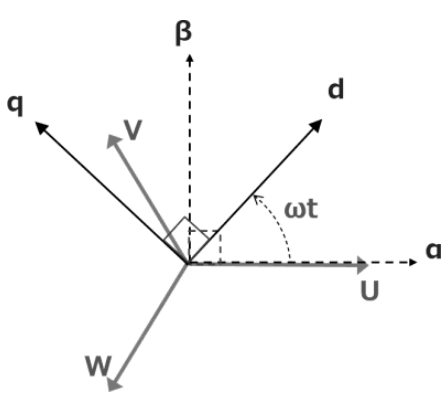
2. 클라크 변환
3상 공간 좌표계는 abc 좌표계 혹은 정지(ω=0) 좌표계(Stationary Reference Frame)라고도 합니다.
3상 좌표계의 a상이 발생시키는 자속의 방향과 일치하는 α축과 이에 직교하는 β축을 갖는 2차원 좌표계로의 변환이다.
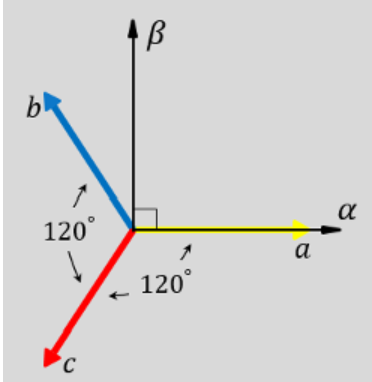
대칭 삼상 교류를 αβ-축 좌표계로 변환하는 것(클락변환)을 고려합니다. 삼상 전류 iu, iv, iw가 αβ-축 좌표계에서 α-축이 u-상 전류와 일치하도록 표현될 때, 전류 iα와 iβ는 식 (1)과 같이 표현 됩니다


위의 행렬 방정식에서 2/3 계수는 상대 변환을 기준으로 한 계수이며, 이는 변환 전후에 상전류의 진폭이 불변임을 의미 합니다. 즉, 순간 전력이 불변인 절대 변환의 경우 계수는 2/3이 됩니다. 여기서는 상대 변환을 기준으로 변환을 수행합니다.
3. Clarke 변환 행렬 유도 (B상: 120°, C상: -120°)
1). 3상 벡터의 방향 설정
Clarke 변환은 3상 전압(Va, Vb, Vc, 즉 A, B, C상)을 α-β 좌표계로 투영합니다. 사용자가 요청한 대로 B상을 α축에서 120°, C상을 -120°(또는 240°)로 설정하여 유도합니다.
- 3상 벡터 방향:
- A상 (Va): α축과 정렬, 0°.
- B상 (Vb): α축에서 120° (θ = 120°).
- C상 (Vc): α축에서 -120° (즉, 240°, θ = -120° 또는 360° - 120°).
- 3상 전압:
- Va=Vm Sin(θ)
- Vb=Vm Sin(θ−2π/3)(120° 뒤짐)
- Vc=Vm Sin(θ+2π/3)(-120° 또는 240°)
- V_m: 전압 진폭 (코드에서 g_k = 0.5).
- θ: 전기 각도 (g_angle).
- 균형 시스템: Va + Vb + Vc = 0.
- α-β 좌표계:
- α축: 0° (A상과 정렬).
- β축: 90° (α축과 직교).
- 각 상의 전압은 α-β 축에 투영되어 v_alpha, v_beta를 형성.
2). α-β 축으로 투영
Clarke 변환은 각 상의 전압을 α-β 축에 투영하여 v_alpha, v_beta를 계산합니다. 투영은 각 상의 방향(0°, 120°, -120°)과 삼각함수(cos, sin)를 사용합니다.
- α축 투영:
- A상: α축과 정렬 (0°), cos(0°) = 1.
- B상: α축에서 120°, cos(120°) = -1/2.
- C상: α축에서 -120° (240°), cos(-120°) = cos(240°) = -1/2.
- v_alpha:
- Valpha = Va⋅cos(0°)+Vb⋅cos(120°)+Vc⋅cos(−120°) = Va⋅1+Vb⋅(−1/2)+Vc⋅(−1/2) = Va−1/2Vb−1/2Vc
- = Va − 1/2 ( Vb + Vc )
- Va + Vb + Vc = 0 적용:
- Vb+Vc = −Va
- Valpha=Va − 1/ 2(−Va) = Va + 1 /2 Va = Va⋅(1+1/2)=Va⋅3/2 = 3/2 Va
- β축 투영:
- A상: β축과 직교 (90°), sin(0°) = 0.
- B상: β축에서 120° - 90° = 30°, sin(120°) = \sqrt{3}/2.
- C상: β축에서 -120° - 90° = -210° (또는 150°), sin(-120°) = -\sqrt{3}/2.
- V_beta:
- Vbeta=Va⋅sin(0°)+Vb⋅sin(120°)+Vc⋅sin(−120°) = Va⋅0+Vb⋅ sqrt(3)/2+Vc⋅(−sqrt(3)/2)= sqrt(3)/2(Vb−Vc)
- 코드에서는 1/sqrt{3}로 정규화:
- 정규화 : sqrt(3)/2(Vb−Vc) ⋅ 3/2 ⋅ 2/3 = 3/2 ⋅ (Vb−Vc)/ sqrt(3)
- 즉 : Vbeta = 3/2 ⋅ (Vb−Vc)/ sqrt(3)
3). 행렬 형태 도출
위 투영 결과를 행렬로 표현:
원 행렬
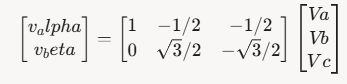

- β축 정규화:

그래서 최종 행렬 ( 3/2 는 단순화 하며 뺀다 )

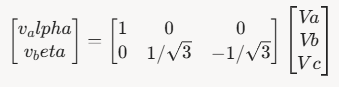
- 코드 구현:
*v_alpha = va_ref;*v_beta = INV_SQRT3 * (vb_ref - vc_ref); // INV_SQRT3 = 1/\sqrt{3} \approx 0.577350269
- v_alpha = va_ref는 Va를 직접 사용.
- v_beta = (vb_ref - vc_ref) / sqrt{3}는 B상과 C상의 차이를 정규화.
4). ---
3. Park 변환
αβ-축 좌표계에서 θ [rad]만큼 이동한 좌표를 dq-축 좌표계로 간주하면, 그 변환 행렬은 식 (2)와 같이 표현됩니다.
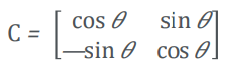
4. dq 변환 ( 클라크 - 박 변환 )
위의 (1)과 (2)에서, dq-축 좌표계에서 id와 iq는 식 (3)과 같이 표현됩니다
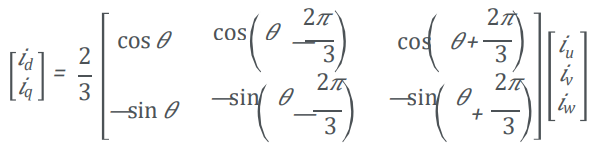
이를 α-β 좌표계, d-q 정지 좌표계 혹은 회전자 좌표계(Rotor Reference Frame)라고 명명합니다.

실제로는 abc 좌표계에서 αβγ 좌표계 혹은 dq0 정지 좌표계로의 변환인데, γ축 혹은 0축은 α-β 평면 혹은 d-q 평면에 수직(법선)한 방향으로 다음 그림과 같이 3x3 정방행렬식을 갖습니다. 여기서 행렬 원소의 2π/3 항은 3상 권선들이 120˚ 등간격으로 배치되었음을 의미합니다.

위 행렬식에서 3번째 행은
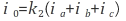
가 되는데 3상 전류 뿐만아니라 전압, 자속 등이 서로간에 120˚의 위상차를 갖는다면 balanced 조건을 만족하여 0이 되어 무시되어 집니다. 이를 0축분 혹은 영상축분이라 부르고 영상축분이 0이 되면 abc 좌표계는 2차원 직교 좌표계로 단순화되어 시스템을 쉽게 다룰 수 있다는 것입니다. 여기서 k1과 k2는 balanced 계수입니다. 일반적으로 변환 전후에 공간 벡터를 크기를 동일하게 하도록 balanced 계수 k1=2/3로 선택하고 생략되지 않는다면 k2=1/2가 됩니다.
또한 회전자(ω=ωr) 좌표계(Rotor Reference Frame)를 회전자의 위치 즉, 기준 자속의 angle(θ)를 알아내고 여기에 자속 성분을 일치시키기 위해서는 angle(θ) 만큼 원점을 중심으로 회전시켜야 합니다. 이와 같은 변환을 Park 변환이라고 하며 d-q 동기 좌표계, de-qe 좌표계 혹은 동기(ω=ωe) 좌표계(Synchronous Reference Frame)라고 명명합니다.
abc 좌표계에서 d-q 좌표계로 바로 변환하려면 위 그림으로부터 다음과 같습니다.

5. 역변환
반대로 d-q 좌표계에서 abc 좌표계로 역변환하려면 행렬식 연산
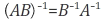
을 이용하여 위 식으로부터 다음과 같습니다. 비정방행렬이라 역행렬(inverse matrix)이 존재하지 않는 것처럼 보이지만 실제로는 d-q좌표계에 영상분(중성)축 0축을 고려한 3x3 정방행렬로 계산하고 balanced 조건하에서 영상분을 다시 제거한 것입니다.

위와 같은 좌표계 변환은 abc 좌표계에서 balanced 조건하에서 전류 뿐만아니라 전압, 자속 등의 변환에 사용할 수 있습니다. 만일 기준 자속의 angle(θ)을 찾아내 실시간으로 회전자 좌표계의 d축과 일치시킨다면 회전자는 고정자의 회전자계와 같은 속도(synchronous)로 아래 그림과 같이 회전하게 됩니다.
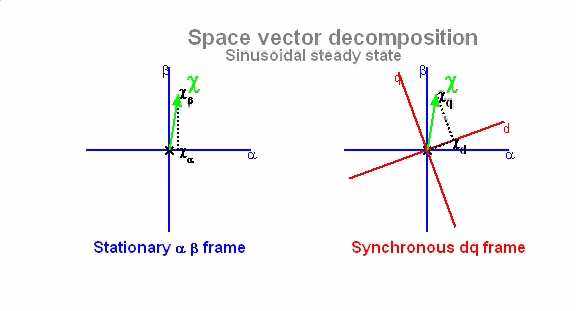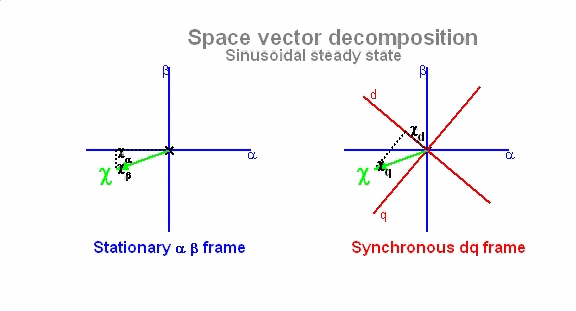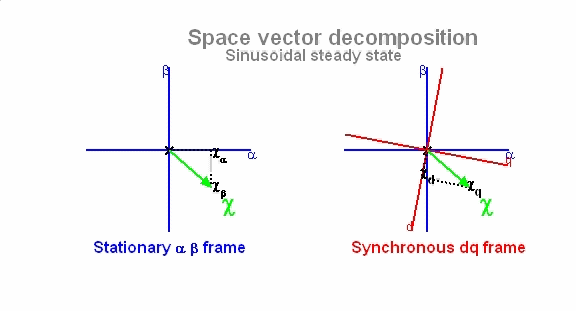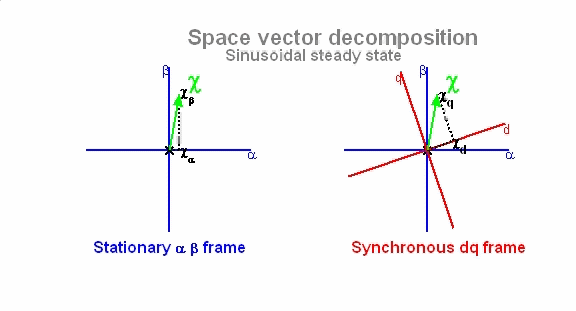
이 때 고정자의 인가되는 전압과 전류 벡터는 회전자의 회전축에서 볼 때 항상 일정한 값으로 보인다는 것입니다. 그러므로 아래 그림에서처럼 d-q 좌표계는 abc와 α-β 좌표계와는 달리 시간에 따라 일정값을 보이게 됩니다. 즉, 이는 3상의 시변 시스템이 2축의 시불변으로 시스템으로 간주되어 이와 같이 변환이 제어를 용이하게 한다는 것입니다.


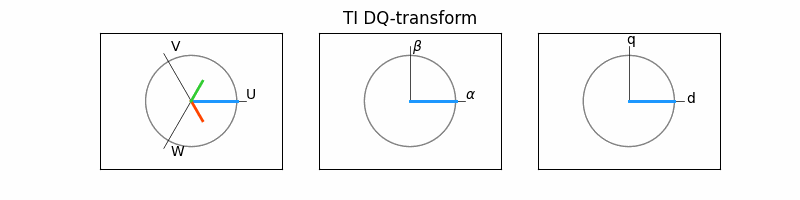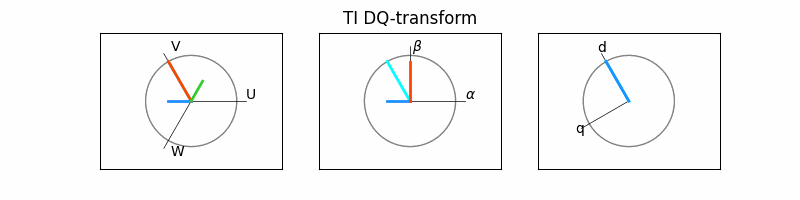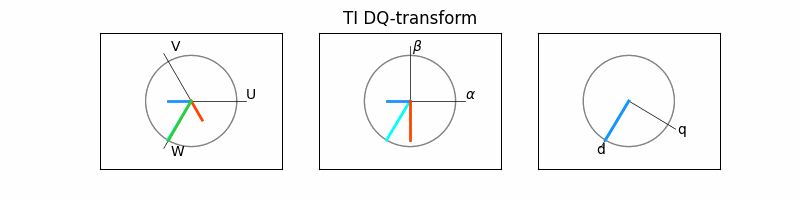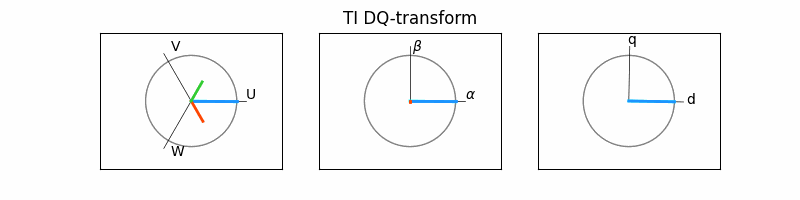
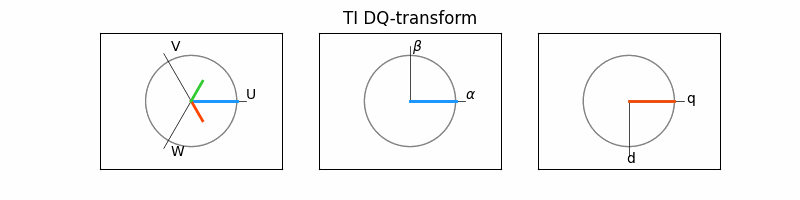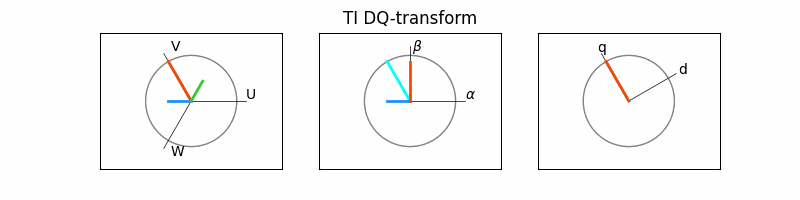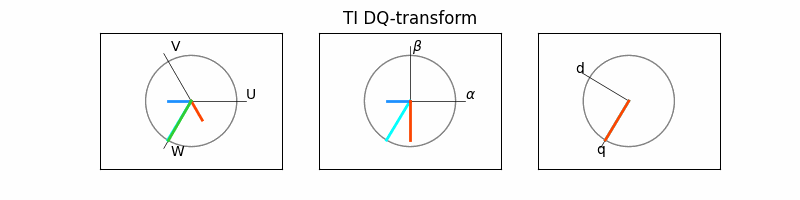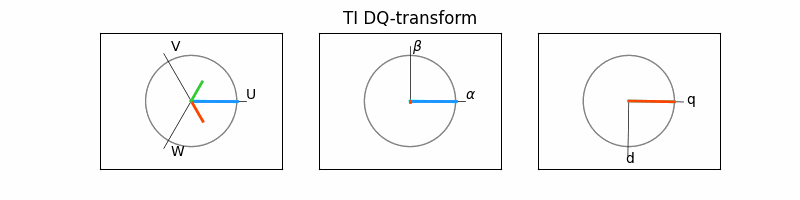
4. 개별 벡터 구하기
SVPWM의 기본적인 원리는 지령 전압과 인접한 2개의 유효 벡터와 영전압을 이용하여 한 주기 동안 평균적으로 합성하는 것입니다. 이를 식으로 표현하면 식 2 또는 식 3과 같이 나타낼 수 있습니다.
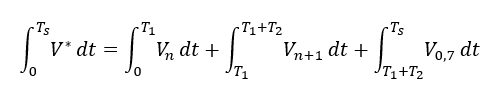
식. 2
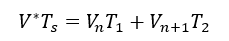
식. 3


그림. 2 SVPWM의 변조 과정
식 2를 벡터 선도로 표현하면 그림 2와 같이 나타낼 수 있습니다. 전압 지령을 생성하는 과정은 그림 2와 같이 3단계입니다. 이는 스위칭 주파수에 결정된 샘플링 주기마다 반복됩니다. 먼저 0~T1에 해당하는 시간 동안 V1의 방향으로 전압을 인가하면, V1(T1/Ts) 크기의 전압이 발생합니다. 그다음으로 T2 시간 동안 V2 방향으로 전압을 인가하면, 지령 전압과 같은 위상과 크기를 맞출 수 있습니다. 마지막으로 T1과 T2 시간의 합이 샘플링 주기보다 작다면 나머지 시간 (식. 8) 동안에는 영 전압 벡터를 인가합니다. 그림 2와 같이 지령 전압 벡터가 sector I 영역에 위치한 경우 식 4와 같이 표현할 수 있습니다.
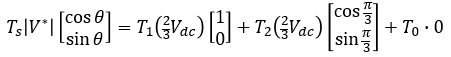
식. 4
이제 식 4를 통해 유효 전압 벡터 인가 시간을 유도하면 각각 식 5와 식 6과 같이 나타낼 수 있습니다.
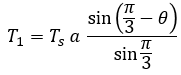
식. 5
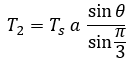
식. 6

식. 7
영 전압 벡터 인가 시간은 식 8과 같이 샘플링 주기에서 T1과 T2를 뺀 시간입니다.
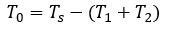
식. 8
SVPWM에서는 유효 전압 벡터 인가 시간의 합이 샘플링 주기 보다 크면 안 됩니다. 따라서 식 9와 같은 조건으로 표현할 수 있습니다.
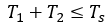
식. 9
식 5와 식 6을 식 9에 대입하면 식 10과 같이 정리할 수 있습니다.
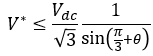
식. 10
식 10의 의미는 지령 전압 벡터의 범위가 그림 3과 같이 노란색 원 안의 영역에 존재한다는 것입니다. 그림 3의 육각형에 내접하는 원은 선형 변조가 가능한 지령 전압의 영역이기도 합니다.
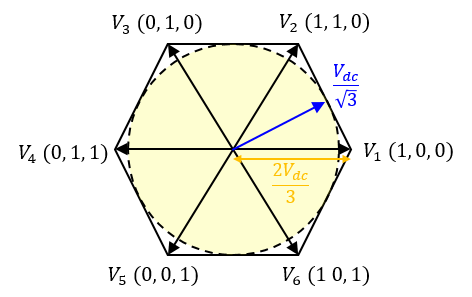
그림. 3 SVPWM에서 제어 가능한 전압 영역
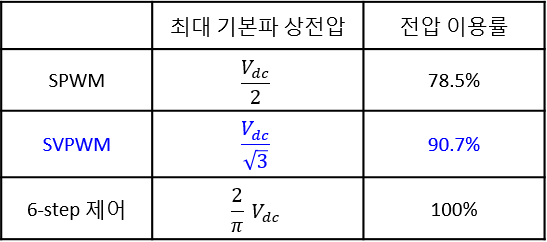
SVPWM의 전압 이용률을 6-step 제어와 SPWM 방식과 비교하면 아래 표와 같습니다. SVPWM 방식이 SPWM 방식보다는 전압 이용률이 높은 것을 확인할 수 있습니다.
참조 :
1. https://sharehobby.tistory.com/entry/Clarke-vs-Park-%EB%B3%80%ED%99%98
2.
3. https://www.switchcraft.org/learning/2017/3/15/space-vector-pwm-intro
Space Vector PWM Intro — Switchcraft
Get rich, smart and famous by understanding the dark arts of space vector pulse width modulation! A must for everyone aspiring to become a star in the drives community!
www.switchcraft.org
4. 요꼬가와 WT5000 설명
'개발 > Motor Inverter' 카테고리의 다른 글
| (3상) 모터 Inverter - 벡터 제어 - 연재 (1) | 2025.07.15 |
|---|---|
| (3상) 모터 Inverter 종류 - SVM, SVPWM - 연재 (7) | 2025.04.03 |
| (3상) 모터 Inverter 종류 - SPWM, Sinusoidal PWM - 연재 (0) | 2025.04.03 |
| (3상) 모터 Inverter 종류 - 6 Step 인버터 - 연재 (0) | 2025.04.03 |
| (3상) 모터 Inverter 종류 - PWM - 연재 (0) | 2025.04.03 |



