(3상) 모터 제어 Inverter - SVM, SVPWM TMS320 소스

3상 모터를 제어 하기 위한 Inverter 방식 종류 (연재)

기본 개념	여러 방식 비교	6 Step, SPWM, SVPWM 등 비교		https://bahk33.tistory.com/230
	PWM 에 대하여			https://bahk33.tistory.com/215
	DQ 변환			https://bahk33.tistory.com/218
	스칼라와 벡터 비교			https://bahk33.tistory.com/229

스칼라	VF ( V/f, VVVF ) 인코더 사용 안함.	Square Wave Inverter, Six Step Inverter		VF,VVVF https://bahk33.tistory.com/216
		SPWM, Sinusoidal PWM		SPWM https://bahk33.tistory.com/217
	슬립 주파수 제어 SFC, Slip Freq Control 인코더 사용
	DTC Direct Torque Control 스위칭 기반	SVM, SVPWM, Space Vector PWM		SVPWM https://bahk33.tistory.com/219 본글 소스 https://bahk33.tistory.com/231
		PTC, MPC 기반 DTC
벡터	FOC Field-Oriented Control	DFOC, 직접 벡터 제어	센서 , 인코더 사용
			센서리스, 인코더 사용 안함
		IFOC 간접 벡터 제어	센서
			센서리스

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

본글 목차

1. 들머리

> SVPWM 을 만드는 TI TMS320F28069 소스 입니다.

> 소스 첨부 및 간단 설명을 합니다.

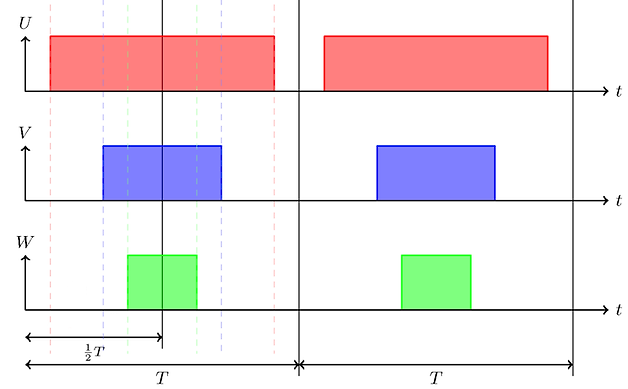
> 먼저 3상 유도 전동기를 돌기기 위해서는 그림 1과 같은 3상 교류 파형을 만들어야 합니다.

> SVPWM 은 그것을 하기 위한 방법중 하나로 설명은 https://bahk33.tistory.com/219 을 보시고, 그림2 와 같은 파형을 만듭니다.

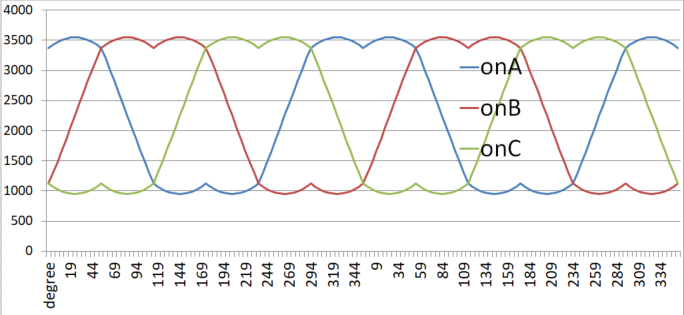
> 본 소스는 그림 2와 같은 파형을 만드는 것 입니다.

2. 주 함수

void fromAngletoSPWM(){
  // 3상 참조 전압 파형
    g_va_ref = g_k * sin(g_rAngle);
    g_vb_ref = g_k * sin(g_rAngle + TWO_PI_OVER_3);
    g_vc_ref = g_k * sin(g_rAngle - TWO_PI_OVER_3);

    // SVPWM 계산및 적용
    do_svpwm(g_va_ref, g_vb_ref, g_vc_ref);

    // 각도 증가
    g_rAngle += 0.8 * DEG_TO_RAD;     // 0.6 ~ 1.0 ?
    if (g_rAngle > TWO_PI) g_rAngle -= TWO_PI;
}

1) 주어진 각(g_rAngle) 에서 만들어야 할 표준 파형( g_va_ref, g_vb_ref, g_vc_ref )

2) 주어진 각 에서 svpwm 만들고 적용 하는 함수 호출 : do_svpwm(g_va_ref, g_vb_ref, g_vc_ref);

3) 주어진 각을 다음 각으로 변경 : g_rAngle += 0.8 * DEG_TO_RAD;

4) 본 함수를 반복적으로 무한히 수행 하면 svpwm 이 됩니다.

3. do_svpwm 함수

// SVPWM 함수
// 1. clarkeTransform : 주어진 참조 전압(va/b/c_ref) 에서 v_alpha, v_beta 계산
// 2. findSector : v_alpha, v_beta 로 부터 섹터 계산
// 3. ActiveVectorTimes: 활성 벡터 시간(T1, T2) 및 제로 벡터 시간(T0) 계산 함수
// 4. abcOnTimes : 온-타임 계산: t_on_A, t_on_B, t_on_C 계산
void do_svpwm(float va_ref, float vb_ref, float vc_ref)
{
    float v_alpha, v_beta; // 알파-베타 좌표계 전압
    float T1, T2, T0; // 활성 벡터 시간(T1, T2) 및 제로 벡터 시간(T0)
    float t_on_A, t_on_B, t_on_C; // 각 상의 온-타임
    int sector; // 현재 섹터 번호 (1~6)
//    float dead_time_value = DEAD_TIME_VALUE;

    // Clarke 변환 호출: 3상 참조 전압을 알파-베타 좌표로 변환
    clarkeTransform(va_ref, vb_ref, vc_ref, &v_alpha, &v_beta);

    // 섹터 결정 함수 호출: v_alpha, v_beta를 사용하여 섹터 판단 이 아니라 각도로 판단.
    sector = findSector();  //    sector = findSector(v_alpha, v_beta);

    // Basic Avtive Vector(V1~V6) On Time(T1, T2) 시간 계산
    ActiveVectorTimes(sector, &T1, &T2, &T0);

    // 온타임 계산 (w, v, u 순서)
    abcOnTimes(sector, T1, T2, T0, &t_on_C, &t_on_B, &t_on_A);

    // Apply to PWM registers
    applyPWM(t_on_A, t_on_B, t_on_C);

#if ( PRINT_MODE == 1 )
    sprintf( prBuf, 
    "%4d,%4d,%6d,%5d,%5d, %5d,%5d, %d, %4d,%4d,%4d, %4d,%4d,%4d\n",
    (int)(g_rAngle*100), (int)(g_rAngle *360 / TWO_PI) ,
    (int)(va_ref*100), (int)(vb_ref*100), (int)(vc_ref*100),
    (int)(v_alpha*100), (int)(v_beta*100), sector,
    (int)T0, (int)T1, (int)T2, 
    (int)t_on_A, (int)t_on_B, (int)t_on_C
     );  // 15개 하면 마지막꺼는 쓰레기
    scia_msg(prBuf);
#endif
    
}

> 5개의 함수 호출로 되어 있읍니다.

> 소스 윗 부분에 그 설명이 있읍니다.

3. clarkeTransform 함수

// Clarke 변환 함수, clarkeTransform : 주어진 참조 전압(va/b/c_ref) 에서 v_alpha, v_beta 계산
// Clarke 변환: 3상(a, b, c) → α-β 좌표계
// B상: α축에서 120°, C상: -120° (240°)
void clarkeTransform(float va_ref, float vb_ref, float vc_ref, float *v_alpha, float *v_beta)
{
    // 3상 참조 전압을 알파-베타 좌표로 변환
    // v_alpha는 va_ref와 동일, v_beta는 vb_ref와 vc_ref의 차이를 sqrt(3)으로 나눔
    *v_alpha = va_ref; // 알파 축 전압은 A상 참조 전압과 동일
    *v_beta = INV_SQRT3 * (vb_ref - vc_ref); // 베타 축 전압은 B상과 C상의 차이를 정규화
}

> Clarke 변환을 하는 부분 입니다.

Clarke 변환에 대하여 자세한것은 DQ변환 ( https://bahk33.tistory.com/218 ) 을 참조 하셔요.

4. 현재 섹터 찾는 함수

int findSector() {
    float theta = g_rAngle * RAD_TO_DEG /60; // g_rAngle * (180/π) / 60
    return (int)floor(theta) + 1; // 섹터 1~6
}

> 알파 ,베타에서 구하는 방법도 있지만, 여기서는 각에 따라 섹터를 구합니다.

> 0 ~ 360 ==> 1 ~ 6 섹터

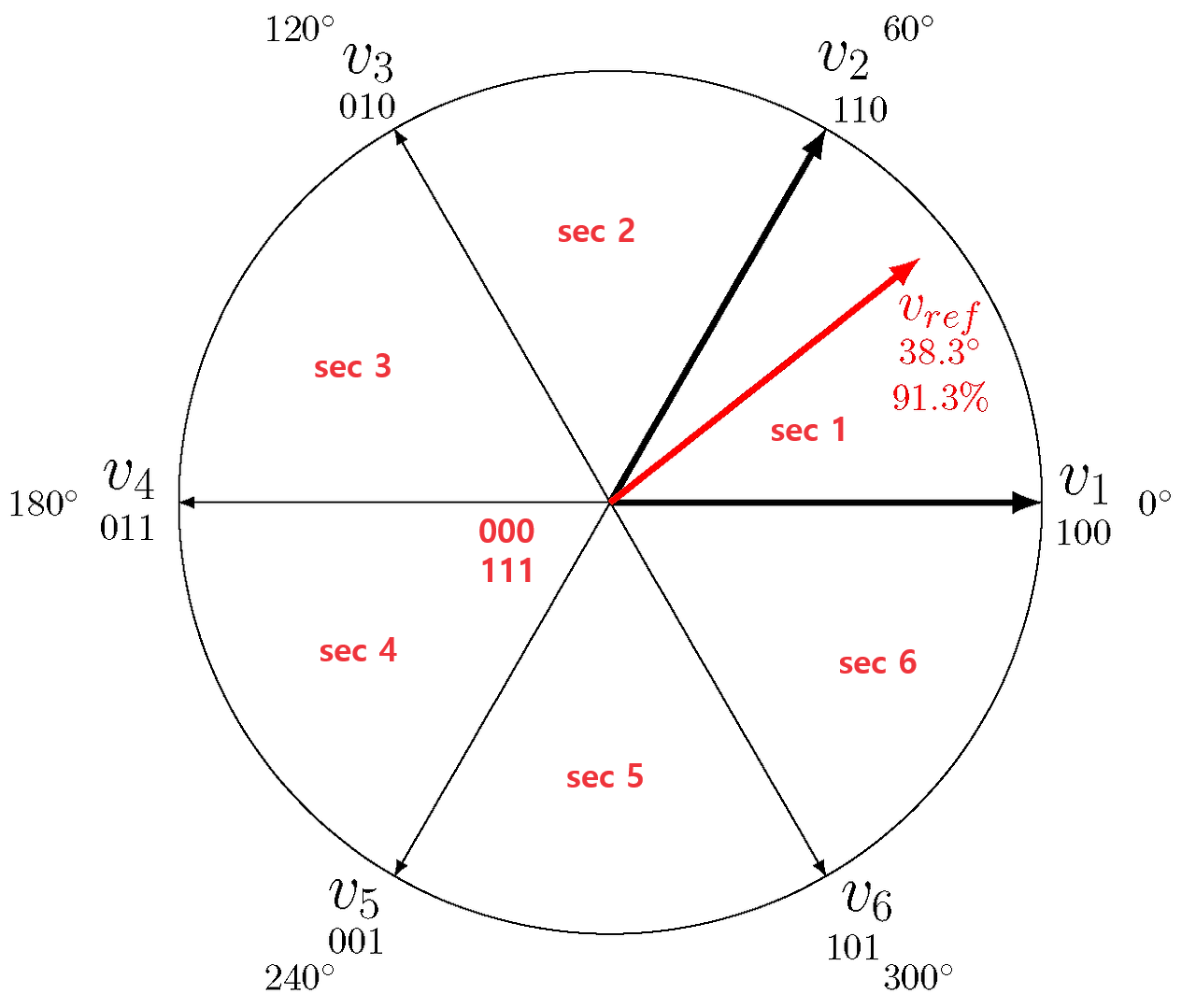
섹터: 공간 벡터 평면은 6개 섹터로 나뉨 (각 60°):

섹터 1: 0°~60° (V1 (100), V2 (110)).
섹터 2: 60°~120° (V2, V3 (010)).
섹터 3: 120°~180° (V3, V4 (011)).
섹터 4: 180°~240° (V4, V5 (001)).
섹터 5: 240°~300° (V5, V6 (101)).
섹터 6: 300°~360° (V6, V1).

> 후기

* 섹터를 찾을때, alpha , beta 로 찾는게 있었는데, 이 alpha 와 beta 가 clarke 변환에 의해 나오고,

또 그 변환을 하기 위하여, 삼상 리퍼런스 ( g_va_ref, g_vb_ref, g_vc_ref ) 가 필요 하다.

* 그런데, 하다 보니 섹터를 찾을때 각으로 찾으니 간단해 진다.

* alpha , beta 로 안 찾고 각으로 찾다 보니, clarkeTransform 함수가 필요 없어 지고,

또한 삼상 리퍼런스 ( g_va_ref, g_vb_ref, g_vc_ref ) 변수 도 필요 없어 지는군... 쩝..

5. 섹터별 Active 벡터 시간 구하기

// SVPWM 시간 계산: g_rAngle 기반, 표준 SVPWM
// SPWM 시간 계산 공식 : T1 = m * Ts * sin(π/3 - θ), T2 = m * Ts * sin(θ), T0 = Ts - T1 - T2.
void ActiveVectorTimes(int sector, float *T1, float *T2, float *T0) {
    float theta, theta_rel,
          m = 2.0f * g_k * PWM_PERIOD / SQRT_3; // 변조 지수

    // Normalize angle to 0 to 2*PI
    while (g_rAngle >= TWO_PI) g_rAngle -= TWO_PI;
    while (g_rAngle < 0.0f) g_rAngle += TWO_PI;

    theta = g_rAngle * RAD_TO_DEG; // 라디안 → 도
    theta = fmodf(theta, 360.0f);   // 실수 나머지
    if (theta < 0) theta += 360.0f; // 음수 를 양수로

    theta_rel = theta - (sector - 1) * 60.0f; // 섹터 내 상대 각도
//    m = 2.0f * g_k * PWM_PERIOD / SQRT_3; // 변조 지수

    // Calculate T1, T2, T0
    *T1 = m * sin(DEG_TO_RAD * (60.0f - theta_rel));
    *T2 = m * sin(DEG_TO_RAD * theta_rel);

//    *T1 = m * sinf((60.0f - theta_rel) * DEG_TO_RAD);   // 실수 sin 함
//    *T2 = m * sinf(theta_rel * DEG_TO_RAD);
    *T0 = PWM_PERIOD - *T1 - *T2;

    if (*T1 < 0) { *T0 = PWM_PERIOD - *T2; *T1 = 0; }
    if (*T2 < 0) { *T0 = PWM_PERIOD - *T1; *T2 = 0; }
    if (*T0 < 0) { *T0 = 0; }
}

1) 각도 0~360 도를 섹터안에서의 각도 0~60 로 바꿉니다.

==> theta_rel = theta - (sector - 1) * 60.0f;

2) 공식에 따라 T1, T2 시간을 구합니다.

섹터: 공간 벡터 평면은 6개 섹터로 나뉨 (각 60°):

섹터 1: 0°~60° (V1 (100), V2 (110)). : T1 은 V1 시간, T2 는 V2 시간
섹터 2: 60°~120° (V2, V3 (010)). : T1 은 V2 시간, T2 는 V3 시간
섹터 3: 120°~180° (V3, V4 (011)). : T1 은 V3 시간, T2 는 V4 시간
섹터 4: 180°~240° (V4, V5 (001)). : T1 은 V4 시간, T2 는 V5 시간
섹터 5: 240°~300° (V5, V6 (101)). : T1 은 V5 시간, T2 는 V6 시간
섹터 6: 300°~360° (V6, V1). : T1 은 V6 시간, T2 는 V1 시간

3) 공식

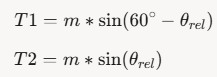
에 대한 설명은 https://bahk33.tistory.com/219 을 참조 하셔요.

3) 구해진 결과 그림

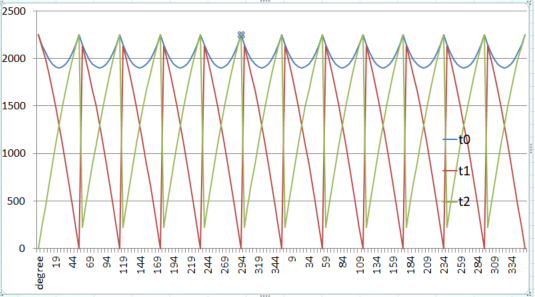
6. 3상 시간 구하기

// 온타임 계산: w(C), v(B), u(A) 순서
// 각 섹터에서 두 활성 벡터(Vi, V(i+1))와 제로 벡터(V0 (000), V7 (111))를 조합하여 참조 벡터(Vref) 생성.
// 스위칭 순서: V0 → Vi → V(i+1) → V7 → V(i+1) → Vi → V0 (대칭 PWM).
// 온타임(t_on_X)은 상단 스위치의 활성 시간을 결정 (AHC 모드: 하단 스위치는 보완적).
void abcOnTimes(int sector, float T1, float T2, float T0, float *t_on_C, float *t_on_B, float *t_on_A) {
//    float max_on, min_on, offset;
//    float offset;
// 0°~60° (V0 → V1 → V2 → V7),  001(U on), 011(U,V on) -> u(a) = t1=t2, v(b)=t2
    switch (sector)  {
    case 1: // 0°~60° (V0 → V1 → V2 → V7 → V2 → V1 → V0)
        *t_on_C = T0 / 2; // w (C상)
        *t_on_B = T0 / 2 + T2; // v (B상)
        *t_on_A = T0 / 2 + T1 + T2; // u (A상)
        break;

    case 2: // 60°~120° (V0 → V2 → V3 → V7 → V3 → V2 → V0)
        *t_on_C = T0 / 2; // w (C상)
        *t_on_B = T0 / 2 + T1 + T2; // v (B상)
        *t_on_A = T0 / 2 + T1; // u (A상)
        break;

    case 3: // 120°~180° (V0 → V3 → V4 → V7 → V4 → V3 → V0)
        *t_on_C = T0 / 2 + T2; // w (C상)
        *t_on_B = T0 / 2 + T1 + T2; // v (B상)
        *t_on_A = T0 / 2; // u (A상)
        break;

    case 4: // 180°~240° (V0 → V4 → V5 → V7 → V5 → V4 → V0)
        *t_on_C = T0 / 2 + T1 + T2; // w (C상)
        *t_on_B = T0 / 2 + T1; // v (B상)
        *t_on_A = T0 / 2; // u (A상)
        break;

    case 5: // 240°~300° (V0 → V5 → V6 → V7 → V6 → V5 → V0)
        *t_on_C = T0 / 2 + T1 + T2; // w (C상)
        *t_on_B = T0 / 2; // v (B상)
        *t_on_A = T0 / 2 + T2; // u (A상)
        break;

    case 6: // 300°~360° (V0 → V6 → V1 → V7 → V1 → V6 → V0)
        *t_on_C = T0 / 2 + T1; // w (C상)
        *t_on_B = T0 / 2; // v (B상)
        *t_on_A = T0 / 2 + T1 + T2; // u (A상)
        break;

        default:
            *t_on_C = *t_on_B = *t_on_A = 0;
            break;
    }

    // 온-타임 경계 처리: 0 ~ PWM_PERIOD 사이로 제한
    *t_on_A = (float)(*t_on_A < 0 ? 0 : (*t_on_A > PWM_PERIOD ? PWM_PERIOD : *t_on_A));
    *t_on_B = (float)(*t_on_B < 0 ? 0 : (*t_on_B > PWM_PERIOD ? PWM_PERIOD : *t_on_B));
    *t_on_C = (float)(*t_on_C < 0 ? 0 : (*t_on_C > PWM_PERIOD ? PWM_PERIOD : *t_on_C));

}

1) 섹터 1 스위칭 패턴과 온타임 계산

> 섹터 1의 스위칭 순서와 각 상의 상단 스위치 상태를 표로 정리:

벡터시간A상 상단B상 상단C상 상단

V0 (000)	T0/2	OFF	OFF	OFF
V1 (100)	T1	ON	OFF	OFF
V2 (110)	T2	ON	ON	OFF
V7 (111)	T0/2	ON	ON	ON
V2 (110)	T2	ON	ON	OFF
V1 (100)	T1	ON	OFF	OFF
V0 (000)	T0/2	OFF	OFF	OFF

A상 상단 스위치 온타임 (t_on_A):
- V1 (100): T1 동안 ON (두 번: 전반부 T1, 후반부 T1).
- V2 (110): T2 동안 ON (두 번: 전반부 T2, 후반부 T2).
- V7 (111): T0/2 동안 ON.
- 총 온타임:
- t_on_A = (T1 + T2 + T0/2) + (T2 + T1) = T0/2 + T1 + T2 + T1 + T2
- 대칭 PWM이므로 전반부(T1 + T2)와 후반부(T1 + T2)를 합산:
- t_on_A = T0/2 + (T1 + T2) + (T1 + T2) => T0/2 + T1 + T2
- (단, V7은 한 번만 계산, 후반부는 대칭이므로 공식은 T0/2 + T1 + T2로 정리).
B상 상단 스위치 온타임 (t_on_B):
- V2 (110): T2 동안 ON (두 번).
- V7 (111): T0/2 동안 ON.
- 총 온타임:
- t_on_B = T0/2 + T2 + T2 => T0/2 + T2

C상 상단 스위치 온타임 (t_on_C):
- V7 (111): C상 상단 ON (T0/2).
- 총 온타임:
- t_on_C = T0/2.

3) 섹터 2 스위칭 패턴과 온타임 계산

섹터 2의 스위칭 순서와 각 상의 상단 스위치 상태를 표로 정리:

벡터시간A상 상단B상 상단C상 상단

V0 (000)	T0/2	OFF	OFF	OFF
V2 (110)	T1	ON	ON	OFF
V3 (010)	T2	OFF	ON	OFF
V7 (111)	T0/2	ON	ON	ON
V3 (010)	T2	OFF	ON	OFF
V2 (110)	T1	ON	ON	OFF
V0 (000)	T0/2	OFF	OFF	OFF

A상 상단 스위치 온타임 (t_on_A):
- V2 (110): A상 상단 ON (T1, 전/후반부).
- V7 (111): A상 상단 ON (T0/2).
- 총 온타임:
- t_on_A = (T1 + T0/2) + (T1) = T0/2 + 2 * T1
- 코드: *t_on_A = T0 / 2 + T1 (대칭 PWM에서 전/후반부 T1 합산을 단순화).
B상 상단 스위치 온타임 (t_on_B):
- V2 (110): B상 상단 ON (T1, 전/후반부).
- V3 (010): B상 상단 ON (T2, 전/후반부).
- V7 (111): B상 상단 ON (T0/2).
- 총 온타임:
- t_on_B = (T1 + T2 + T0/2) + (T2 + T1) = T0/2 + T1 + T2 + T1 + T2 = T0/2 + 2 * T1 + 2 * T2
- 대칭 PWM에서 전/후반부 합산:
- t_on_B = T0/2 + (T1 + T2) + (T1 + T2) => T0/2 + T1 + T2
C상 상단 스위치 온타임 (t_on_C):
- V7 (111): C상 상단 ON (T0/2).
- 총 온타임:
- t_on_C = T0/2.

4). 섹터 3 스위칭 패턴과 온타임 계산

섹터 3의 스위칭 순서와 각 상의 상단 스위치 상태를 표로 정리:

벡터시간A상 상단B상 상단C상 상단

V0 (000)	T0/2	OFF	OFF	OFF
V3 (010)	T1	OFF	ON	OFF
V4 (011)	T2	OFF	ON	ON
V7 (111)	T0/2	ON	ON	ON
V4 (011)	T2	OFF	ON	ON
V3 (010)	T1	OFF	ON	OFF
V0 (000)	T0/2	OFF	OFF	OFF

A상 상단 스위치 온타임 (t_on_A):
- V7 (111): A상 상단 ON (T0/2).
- 총 온타임:
- t_on_A = T0/2.
B상 상단 스위치 온타임 (t_on_B):
- V3 (010): B상 상단 ON (T1, 전/후반부).
- V4 (011): B상 상단 ON (T2, 전/후반부).
- V7 (111): B상 상단 ON (T0/2).
- 총 온타임:
- t_on_B = (T1 + T2 + T0/2) + (T2 + T1) = T0/2 + T1 + T2 + T1 + T2 = T0/2 + 2 * T1 + 2 * T2
- 대칭 PWM에서 전/후반부 합산:
- t_on_B = T0/2 + (T1 + T2) + (T1 + T2) => T0/2 + T1 + T2
C상 상단 스위치 온타임 (t_on_C):
- V4 (011): C상 상단 ON (T2, 전/후반부).
- V7 (111): C상 상단 ON (T0/2).
- 총 온타임:
- t_on_C = (T2 + T0/2) + (T2) = T0/2 + T2 + T2 = T0/2 + 2 * T2
- 대칭 PWM에서 전/후반부 합산:
- t_on_C = T0 / 2 + T2

5). 섹터 4 스위칭 패턴과 온타임 계산

섹터 4의 스위칭 순서와 각 상의 상단 스위치 상태를 표로 정리:

벡터시간A상 상단B상 상단C상 상단

V0 (000)	T0/2	OFF	OFF	OFF
V4 (011)	T1	OFF	ON	ON
V5 (001)	T2	OFF	OFF	ON
V7 (111)	T0/2	ON	ON	ON
V5 (001)	T2	OFF	OFF	ON
V4 (011)	T1	OFF	ON	ON
V0 (000)	T0/2	OFF	OFF	OFF

A상 상단 스위치 온타임 (t_on_A):
- V7 (111): A상 상단 ON (T0/2).
- 총 온타임:
- t_on_A = T0/2 .
B상 상단 스위치 온타임 (t_on_B):
- V4 (011): B상 상단 ON (T1, 전/후반부).
- V7 (111): B상 상단 ON (T0/2).
- 총 온타임:
- t_on_B = (T1 + T0/2) + (T1) = T0/2 + T1 + T1 = T0/2 + 2 * T1
- 대칭 PWM에서 전/후반부 합산:
- t_on_B = T0/2 + T1.
C상 상단 스위치 온타임 (t_on_C):
- V4 (011): C상 상단 ON (T1, 전/후반부).
- V5 (001): C상 상단 ON (T2, 전/후반부).
- V7 (111): C상 상단 ON (T0/2).
- 총 온타임:
- t_on_C = (T1 + T2 + T0/2) + (T2 + T1) = T0/2 + T1 + T2 + T1 + T2 = T0/2 + 2 * T1 + 2 * T2
- 대칭 PWM에서 전/후반부 합산:
- t_on_C = T0/2 + (T1 + T2) + (T1 + T2) = T0/2 + T1 + T2

6). 섹터 5 스위칭 패턴과 온타임 계산

섹터 5의 스위칭 순서와 각 상의 상단 스위치 상태를 표로 정리:

벡터시간A상 상단B상 상단C상 상단

V0 (000)	T0/2	OFF	OFF	OFF
V5 (001)	T1	OFF	OFF	ON
V6 (101)	T2	ON	OFF	ON
V7 (111)	T0/2	ON	ON	ON
V6 (101)	T2	ON	OFF	ON
V5 (001)	T1	OFF	OFF	ON
V0 (000)	T0/2	OFF	OFF	OFF

A상 상단 스위치 온타임 (t_on_A):
- V6 (101): A상 상단 ON (T2, 전/후반부).
- V7 (111): A상 상단 ON (T0/2).
- 총 온타임:
- t_on_A = (T2 + T0/2) + (T2) = T0/2 + T2 + T2 = T0/2 + 2 * T2
- 대칭 PWM에서 전/후반부 합산:
- t_on_A = T0/2 + T2
B상 상단 스위치 온타임 (t_on_B):
- V7 (111): B상 상단 ON (T0/2).
- 총 온타임:
- t_on_B = T0/2 .
C상 상단 스위치 온타임 (t_on_C):
- V5 (001): C상 상단 ON (T1, 전/후반부).
- V6 (101): C상 상단 ON (T2, 전/후반부).
- V7 (111): C상 상단 ON (T0/2).
- 총 온타임:
- t_on_C = (T1 + T2 + T0/2) + (T2 + T1) = T0/2 + T1 + T2 + T1 + T2 = T0/2 + 2 * T1 + 2 * T2
- 대칭 PWM에서 전/후반부 합산:
- t_on_C = T0/2 + (T1 + T2) + (T1 + T2) = T0/2 + T1 + T2.

7) 섹터 6 스위칭 패턴과 온타임 계산

섹터 6의 스위칭 순서와 각 상의 상단 스위치 상태를 표로 정리:

벡터시간A상 상단B상 상단C상 상단

V0 (000)	T0/2	OFF	OFF	OFF
V6 (101)	T1	ON	OFF	ON
V1 (100)	T2	ON	OFF	OFF
V7 (111)	T0/2	ON	ON	ON
V1 (100)	T2	ON	OFF	OFF
V6 (101)	T1	ON	OFF	ON
V0 (000)	T0/2	OFF	OFF	OFF

3.1. 온타임 계산

A상 상단 스위치 온타임 (t_on_A):
- V6 (101): A상 상단 ON (T1, 전/후반부).
- V1 (100): A상 상단 ON (T2, 전/후반부).
- V7 (111): A상 상단 ON (T0/2).
- 총 온타임:
- t_on_A = (T1 + T2 + T0/2) + (T2 + T1) = T0/2 + T1 + T2 + T1 + T2 = T0/2 + 2 * T1 + 2 * T2
- 대칭 PWM에서 전/후반부 합산:
- t_on_A = T0/2 + (T1 + T2) + (T1 + T2) = T0/2 + T1 + T2
B상 상단 스위치 온타임 (t_on_B):
- V7 (111): B상 상단 ON (T0/2).
- 총 온타임:
- t_on_B = T0/2
C상 상단 스위치 온타임 (t_on_C):
- V6 (101): C상 상단 ON (T1, 전/후반부).
- V7 (111): C상 상단 ON (T0/2).
- 총 온타임:
- t_on_C = (T1 + T0/2) + (T1) = T0/2 + T1 + T1 = T0/2 + 2 * T1
- 대칭 PWM에서 전/후반부 합산:
- t_on_C = T0/2 + T1.

8) 구해진 시간은 다음 그림과 갈읍니다.

7. PWM 값 적용 하기

// Function to apply PWM settings (TMS320F28069 ePWM module)
void applyPWM(float t_on_A, float t_on_B, float t_on_C)
{
   Uint16 cmpa_A, cmpa_B, cmpa_C;

    // 센터 정렬 모드에서 CMPA 값 계산: 온-타임의 절반
    cmpa_A = t_on_A / 2.0; //    cmpa_A = (Uint16)(D_TBPRD * t_on_A / PWM_PERIOD); // EPWM1A (A-phase)
    cmpa_B = t_on_B / 2.0; //    cmpa_B = (Uint16)(D_TBPRD * t_on_B / PWM_PERIOD); // EPWM2A (B-phase)
    cmpa_C = t_on_C / 2.0; //    cmpa_C = (Uint16)(D_TBPRD * t_on_C / PWM_PERIOD); // EPWM3A (C-phase)

    // ePWM 비교 레지스터 업데이트
    EPwm1Regs.CMPA.half.CMPA = (Uint16)cmpa_A; // A상 PWM 듀티 설정
    EPwm2Regs.CMPA.half.CMPA = (Uint16)cmpa_B; // B상 PWM 듀티 설정
    EPwm3Regs.CMPA.half.CMPA = (Uint16)cmpa_C; // C상 PWM 듀티 설정
}

8. 전체 소스 첨부

> 위 글은 기본적으로 25/7/ 23 일자 소스를 기준으로 합니다.

ti-tms320f28069-svpwm-250723.zip

0.62MB

>250724

- 클라크 변환이 섹터 구하는 데 쓰이는데, 섹터를 각도에서 직접 구하다 보니 필요 없어 뺌

- 가변 속도 추가

ti-tms320f28069-svpwm-250724.zip

0.63MB

9 vvvf (Variable Voltage Variable Frequency) 구현

1) 바뀐, 추가된 소스 부분

SPWM ( Sinusoidal PWM ) 에서 했던 VVVF 를 여기서도 해 보았읍니다. 뭔 의미가 있는지 모르지만,

속도를 변화 하게 하고, 속도에 따라 전압을 달리 주는 거 입니다.

#define LOW_FREQ_BOOST  0.15f    // 저주파수에서 변조 지수 boost
#define MAX_MI          0.866f  // 과변조 방지를 위해 변조 지수 제한 (3차 고조파 제외 시 최대 0.866)

void set_freq_n_step(unsigned char isUp){   // 출력 주파수와 각변화량 설정:0: 초기 값, 1: 증가
    switch ( isUp){
    case 0:  g_AddRAngle = 0.8; break;      // 0.8 초기 값 설정
    case 1:
        g_AddRAngle *= ( g_AddRAngle < 0.5 ) ?  3.0 :  1.3;  // 0.5 보다 작음 3 , 아님 1.3 곱함
        if( g_AddRAngle > 3.7 ) {   // 3.5 최대 각속도 보다 크면,
            g_AddRAngle = 0.001 ;     // 0.001 최소값으로 바꾼다.
        }
        break;
    }
//    g_AddRAngle = 3.0;  // 최소 mi test

    ////////////////////////////  vvvf 고려한, 변조 지수 
    // V/f 제어로 변조 지수 계산 
    // g_AddRAngle  g_mi    mi= ((ara + 1) * 2) / 10 
    //  0            0.0 -> Min 
    //  1            0.4
    //  2           0.8
    //  3           1.2 -> Max  0.866f
    g_mi =  g_AddRAngle * 0.4;

    // 저주파수에서 전압 강하 보상을 위해 boost 적용
    if (g_mi < LOW_FREQ_BOOST) g_mi = LOW_FREQ_BOOST;  

    // 과변조 방지를 위해 변조 지수 제한 (3차 고조파 제외 시 최대 0.866)
    if (g_mi > MAX_MI) g_mi = MAX_MI;       // MAX_MI == 0.866f
}

2) 각속도가 적을때 ( 0.1 도씩 변화, modulation index = 0.15),

클때 ( 3.0 도씩 변화 , modulation index = 0.8659 ) 비교

> 결과적으로 속도가 느리면, modulation index 가 적어 지고 그럼 Active 벡터가 작어 지고, 3상 켜지는 시간 폭 변화가 적어 지는 것을 볼 수 있읍니다.

> Active Ventor (T1, T2), 와 제로벡터 ( T0 ) 비교

- 속도 느릴때 : 활성 벡터 값의 변화가 적고, 제로 벡터 부분이 크다

- 속도 빠를때 : 활성 벡터 값의 변화가 크고, 제록 벡터 부분이 작다

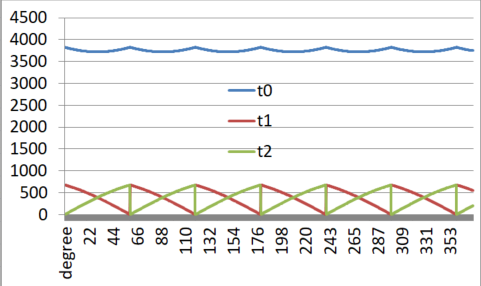
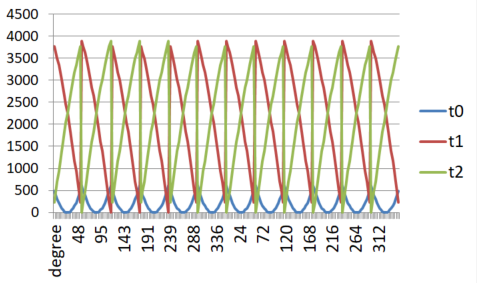
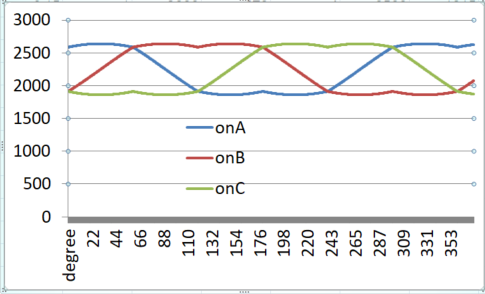
0.1 도씩 변화 , modulation index = 0.15 < 벡터 크기 비교 > 3.0 도씩 변화 , modulation index = 0.8659

> 3상 온타임 비교

- 속도 느릴때 : 사인파(?) 의 변화가 적다

- 속도 빠를때 : 사인파(?) 의 변화가 크다

0.1 도씩 변화 , modulation index = 0.15 < 3삼 온타임 비교 > 3.0 도씩 변화 , modulation index = 0.8659

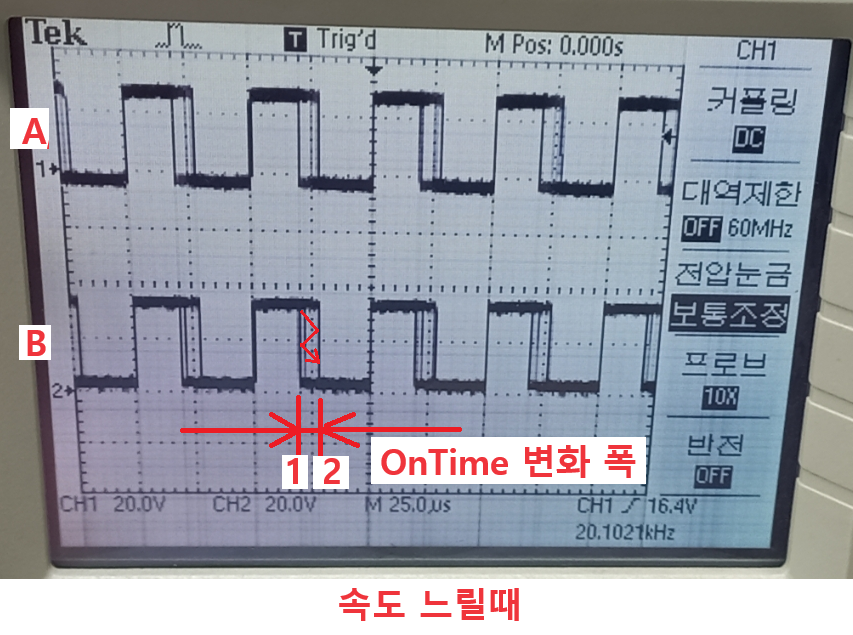
> 오실로스코프 사진 ( 0,1 도씩 변화 아니지만, 어째든 느린거와 3.0 도씩 변화 아니지만 어째든 빠른거 비교 )

- 속도 느릴때 : 왼쪽 그림 1 과 2

회전수가 느린 만큼 1과 2 사이를 천천이 왔다 갔다 한다.

mi 를 작게 하여 on time 변화 폭(1, 2 간격) 이 적다,

- 속도 빠를때 :

회전수 빠른 만큼 3과 4 사이를 빠르게 왔다 갔다 한다.

mi 를 크게 하여 on time 변화 폭(3,4 간격)이 크다,

> vvvf 소스 첨부 합니다.

RAM 에서 돌아 가는거

ti-tms320f28069-svpwm-250726.zip

0.77MB

FLASH 에서 돌아가는거

ti-tms320f28069-svpwm-251117.zip

1.18MB

'개발 > Motor Inverter' 카테고리의 다른 글

(3상) 모터 제어 Inverter - 방법 비교 pwm, spwm,svpwm,foc (4)	2025.07.16
(3상) 모터 Inverter - 벡터 제어 - 연재 (1)	2025.07.15
(3상) 모터 Inverter 종류 - SVM, SVPWM - 연재 (7)	2025.04.03
(3상) 모터 Inverter 종류 - dq 변환 (Clarke + Park 변환) - 연재 (0)	2025.04.03
(3상) 모터 Inverter 종류 - SPWM, Sinusoidal PWM - 연재 (0)	2025.04.03

즐기며

(3상) 모터 제어 Inverter - SVM, SVPWM TMS320 소스

1) 섹터 1 스위칭 패턴과 온타임 계산

3) 섹터 2 스위칭 패턴과 온타임 계산

4). 섹터 3 스위칭 패턴과 온타임 계산

5). 섹터 4 스위칭 패턴과 온타임 계산

6). 섹터 5 스위칭 패턴과 온타임 계산

7) 섹터 6 스위칭 패턴과 온타임 계산

3.1. 온타임 계산

'개발 > Motor Inverter' 카테고리의 다른 글

티스토리툴바

(3상) 모터 제어 Inverter - SVM, SVPWM TMS320 소스

1) 섹터 1 스위칭 패턴과 온타임 계산

3) 섹터 2 스위칭 패턴과 온타임 계산

4). 섹터 3 스위칭 패턴과 온타임 계산

5). 섹터 4 스위칭 패턴과 온타임 계산

6). 섹터 5 스위칭 패턴과 온타임 계산

7) 섹터 6 스위칭 패턴과 온타임 계산

3.1. 온타임 계산

'개발 > Motor Inverter' 카테고리의 다른 글

관련글

티스토리툴바