3상 모터를 제어 하기 위한 Inverter 방식 종류 (연재)
| 기본 개념 | 여러 방식 비교 | 6 Step, SPWM, SVPWM 등 비교 | https://bahk33.tistory.com/230 | |
| PWM 에 대하여 | https://bahk33.tistory.com/215 | |||
| DQ 변환 | https://bahk33.tistory.com/218 | |||
| 스칼라와 벡터 비교 | https://bahk33.tistory.com/229 | |||
| 스칼라 | VF ( V/f, VVVF ) 인코더 사용 안함. |
Square Wave Inverter, Six Step Inverter |
VF,VVVF https://bahk33.tistory.com/216 | |
| SPWM, Sinusoidal PWM | SPWM https://bahk33.tistory.com/217 | |||
| 슬립 주파수 제어 SFC, Slip Freq Control 인코더 사용 |
||||
| DTC Direct Torque Control 스위칭 기반 |
SVM, SVPWM, Space Vector PWM | 본글 SVPWM https://bahk33.tistory.com/219 소스 https://bahk33.tistory.com/231 |
||
| PTC, MPC 기반 DTC | ||||
| 벡터 | FOC Field-Oriented Control |
DFOC, 직접 벡터 제어 |
센서 , 인코더 사용 | |
| 센서리스, 인코더 사용 안함 |
||||
| IFOC 간접 벡터 제어 |
센서 | |||
| 센서리스 | ||||
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
목차
1. 소개
2. 3상 전압
3. 2레벨 인버터의 토폴로지
4. 출력 전압 합성
5. 개념 설명
6. 한 섹터 안에서의 표현
7. 3차 고조파 주입
8. 변조지수, Modulation index, M
9. 과변조
==============================
1. 소개
- 공간 벡터 펄스 폭 변조(SV-PWM)는 주어진 전압 벡터를 3상 전기 모터(영구 자석 또는 유도 전동기)에 인가하는 데 사용되는 변조 방식입니다. 이 기술의 목표는 안정적인 DC 전압을 사용하여 6개의 스위치(예: 트랜지스터, FET, IGBT 등)를 통해 주파수와 진폭을 조절할 수 있는 3상 사인파형을 만드는 것입니다.
- 사용 가능한 전압 레벨은 DC 링크 전압뿐이며, 이는 일정하다고 가정할 수 있습니다.
- 사용 가능한 전압 각도는 6개뿐이며 중간 지점이 없습니다. 모터를 회전시키려면 한 번에 60도씩 건너뛰는 것이 아니라 부드럽게 회전하는 전압 벡터가 필요합니다.
2. 공급되는 3상 전압
그리드에서 공급된 3상 전압은 아래 애니메이션과 같습니다. 이는 유도기가 그리드에 직접 연결될 때 발생하는 현상입니다.
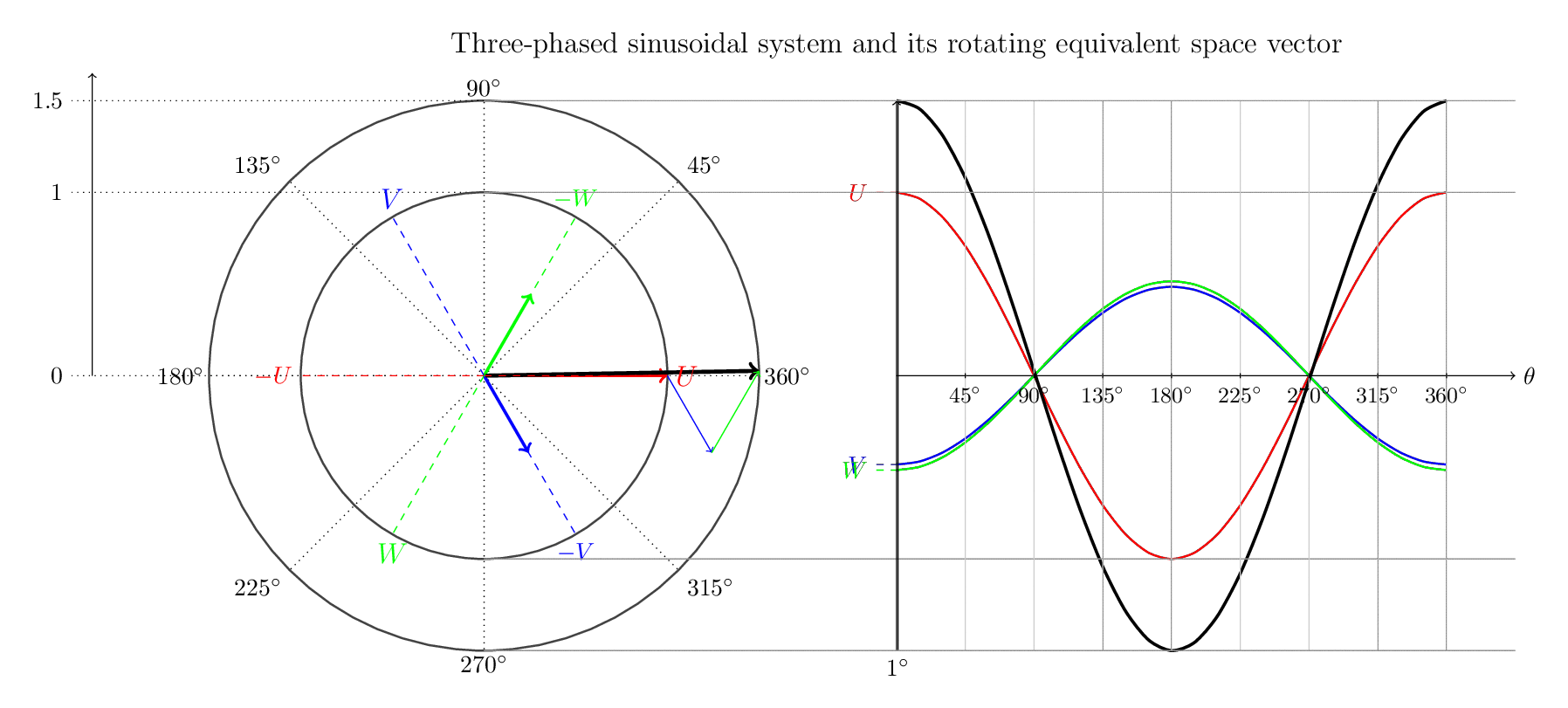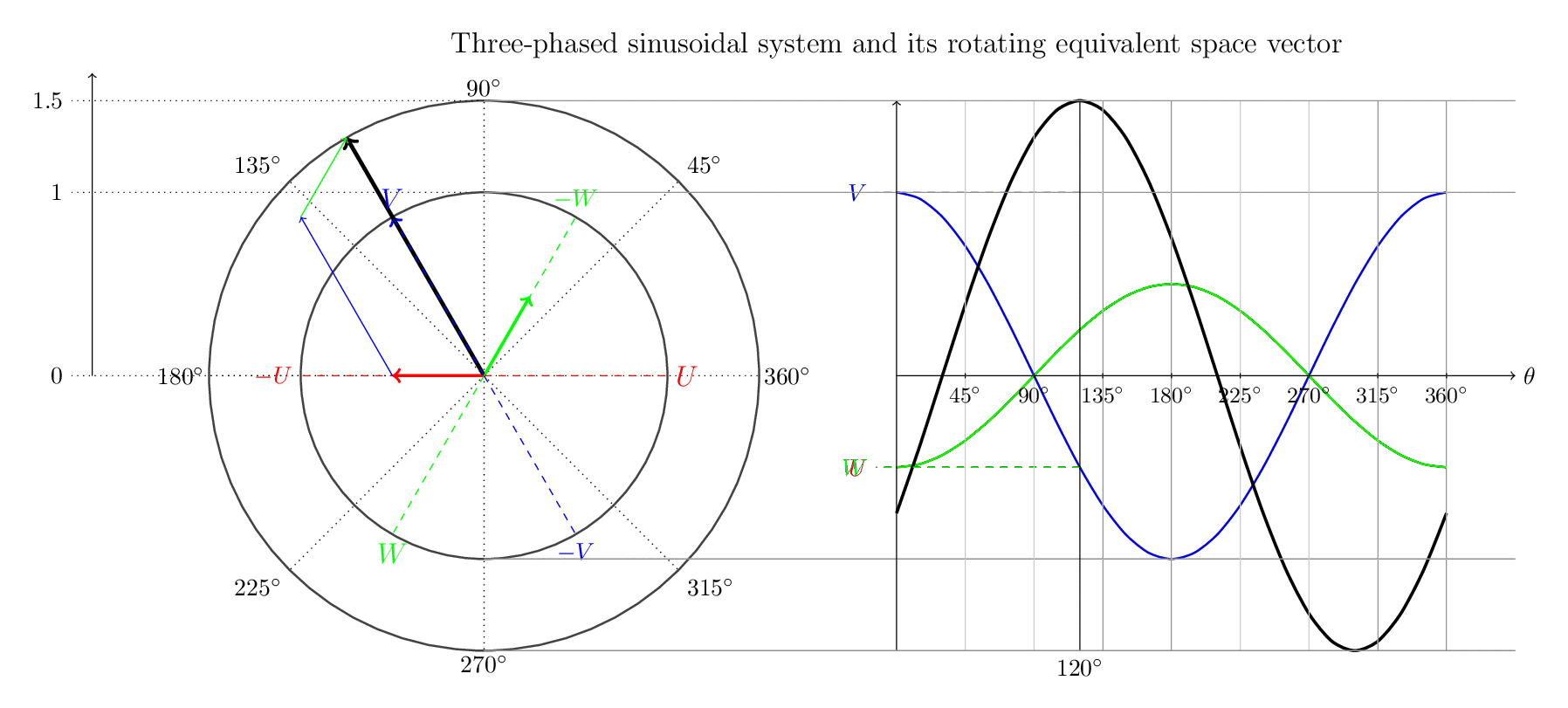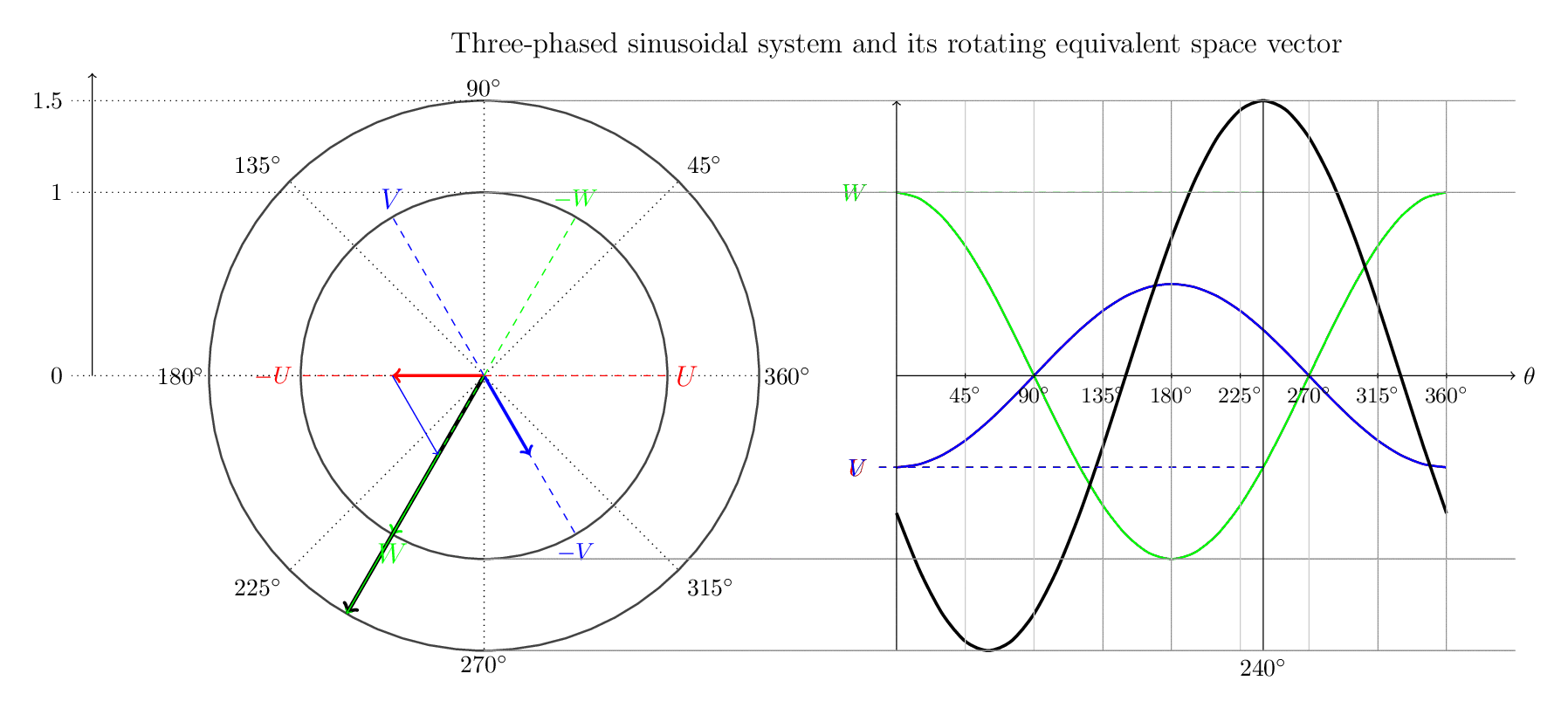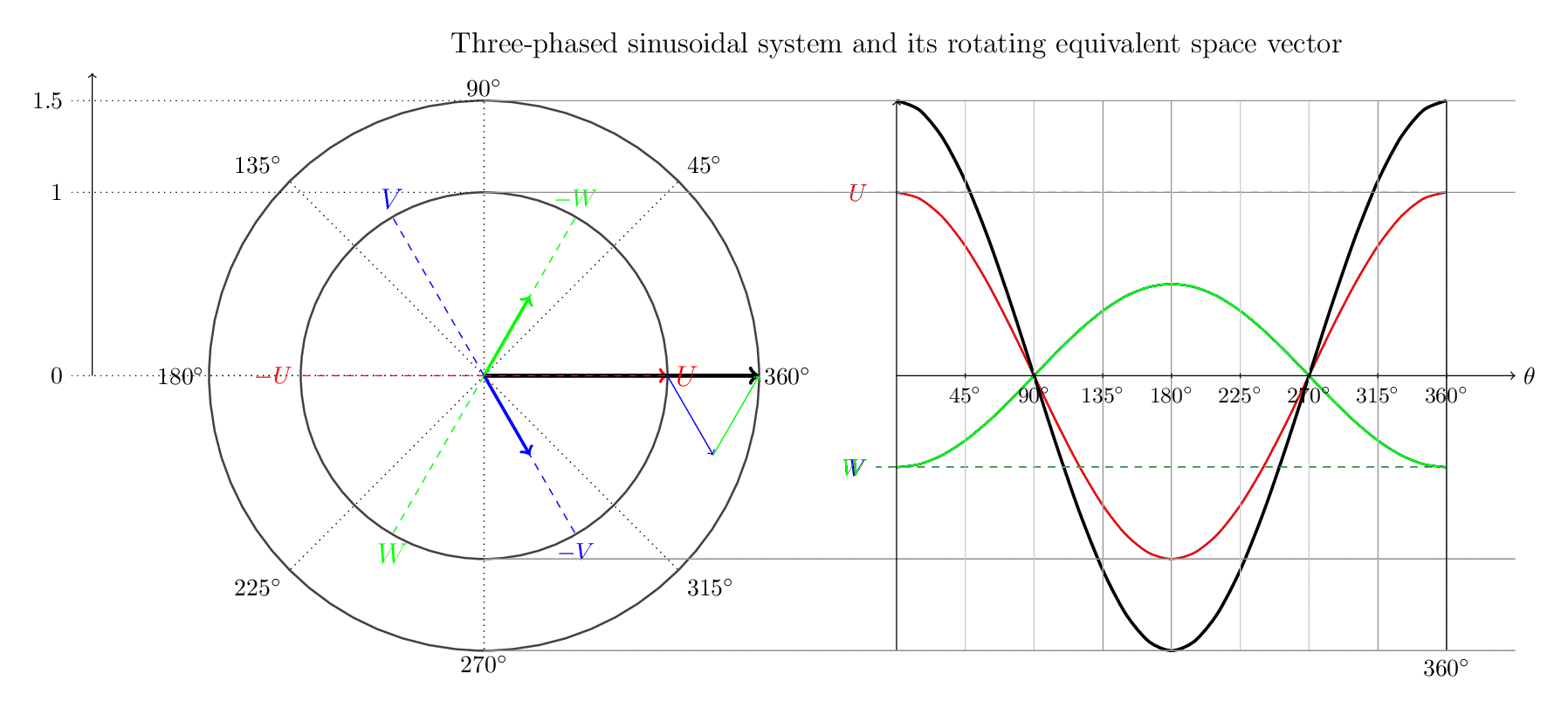
3단계 시스템은 서로 다르지만 동일한 두 가지 형식을 사용하여 설명됩니다.
- 1. 3개의 위상과 그 벡터 합( 공간 벡터)을 보여주는 벡터 다이어그램입니다 .
- 2. 일반적인 순간 사인파 표현과 그에 따른 공간 벡터도 보여줍니다.
3. 2레벨 인버터의 토폴로지
2단계 인버터는 간단하고 저렴하기 때문에 오늘날 가장 많이 사용되는 토폴로지입니다. 상위(4~) 레벨 컨버터는 대부분 고전압 애플리케이션에 사용되며 본 에서는 다루지 않습니다.
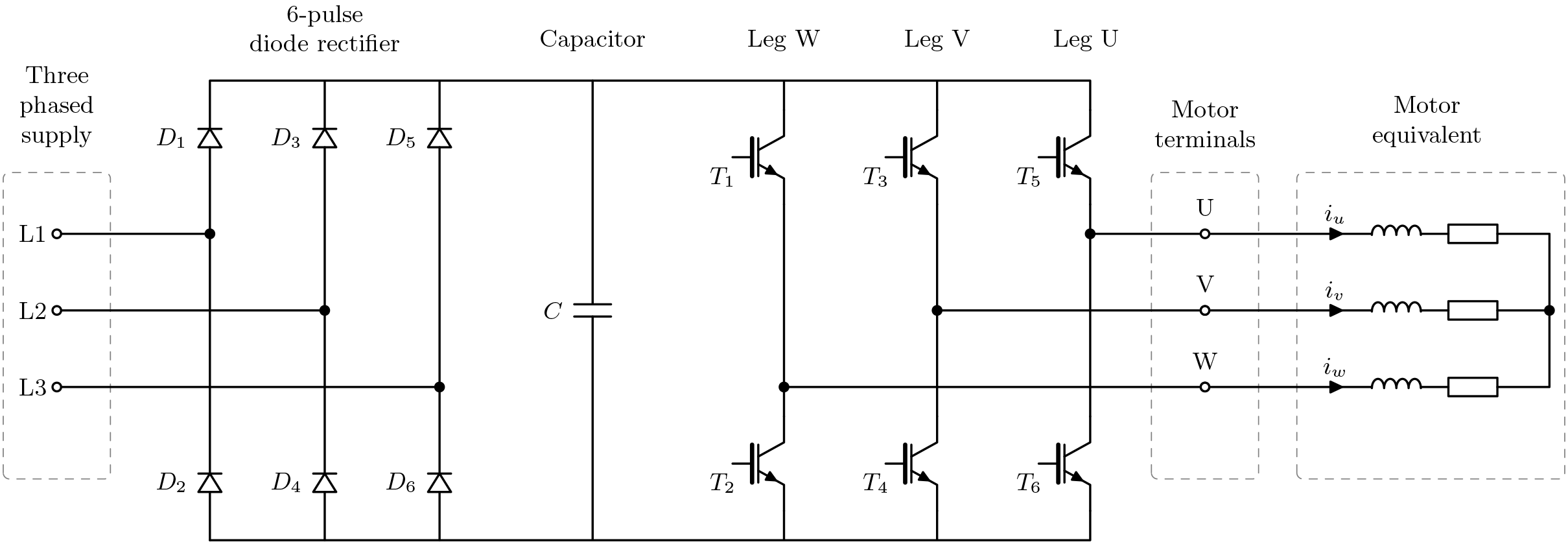
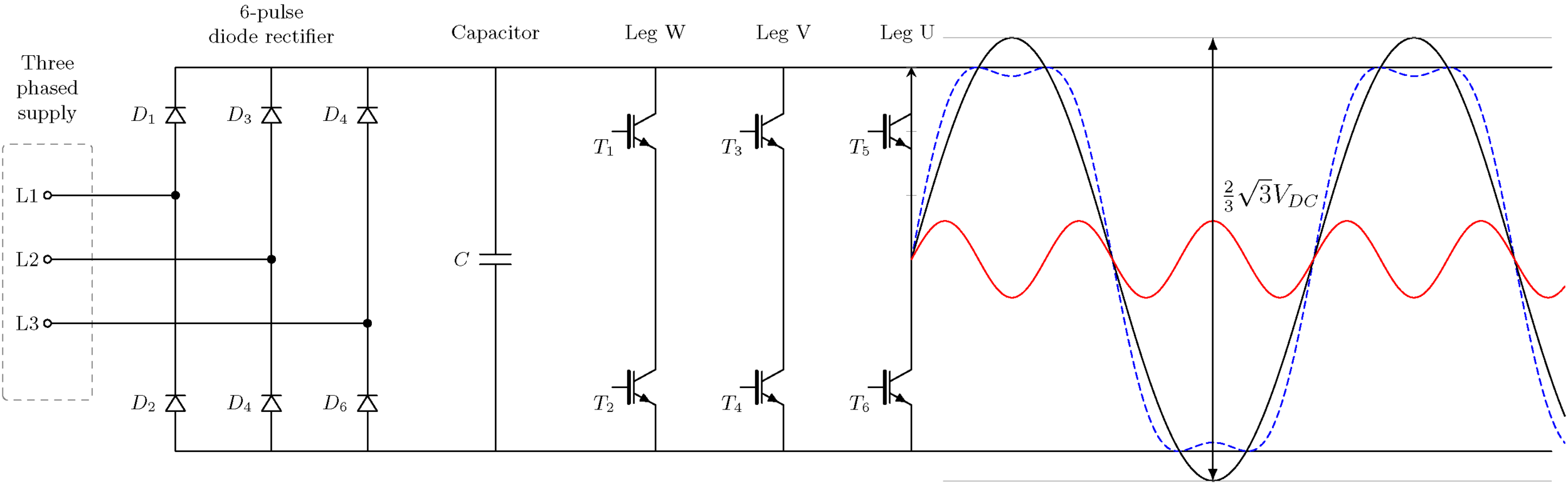
위의 회로도는 잘 알려지고 널리 사용되는 인버터 토폴로지입니다. 왼쪽에서 오른쪽으로 다음이 표시됩니다.
- 3상 공급 장치 및 3상 다이오드 정류기.
- 에너지 저장 및 전압 안정화를 위한 DC 링크 커패시터.
- 6개의 트랜지스터가 있는 인버터 브리지.
- 3개의 출력 단자 및 성형 결선(비접지) 유도 전동기 등가 회로.
표시되지 않은 항목: 스너버 회로, 트랜지스터 양단의 역병렬 다이오드 및 모터의 역기전력(back-EMF).
공간 벡터 PWM의 사용법을 더 잘 이해하기 위해 위 회로도를 크게 단순화할 수 있습니다.
- 첫째, DC 링크 전압은 일정하도록 단순화할 수 있습니다. 일반적으로 부하에 따라 변동하지만 이 글에서 다루는 시간 프레임 동안에는 그다지 많이 변하지 않습니다. 따라서 공급 장치 및 다이오드 정류기는 이 글의 나머지 부분에서는 표시되지 않습니다.
- 둘째, 인버터 브리지의 각 레그는 두 개의 브리지 레그 트랜지스터를 하나의 단일 SPDT 스위치로 교체하여 단순화할 수 있으며, 이는 상단 또는 하단 트랜지스터가 하나만 연결 되어 있음을 나타냅니다. 한쪽 레그의 두 트랜지스터가 모두 열려 있는 시나리오는 필요하지 않습니다. 또한 두 트랜지스터가 모두 닫혀 있는 시나리오는 DC 링크가 단락되어 우리 모두가 집에 가서 새 부품을 주문해야 함을 의미합니다.
두 개의 트랜지스터에서 하나의 SPDT 스위치로 단순화하는 것은 각 브리지 레그에서 한 개의 트랜지스터만 주어진 시간에 닫을 수 있고, 3상 전류가 흐르도록 하려면 각 레그에서 한 개의 트랜지스터를 닫아야 하기 때문에 가능합니다 . 또한 양방향 전류 흐름을 허용하기 위해 각 트랜지스터에 항상 역병렬 다이오드가 있습니다.
단순화된 개략도는 아래와 같습니다.

*. 참고: 스위치 종류
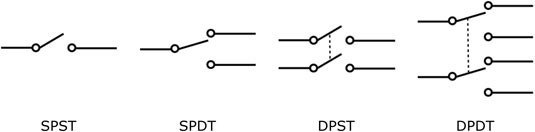
- SPST (Single Pole, Single Throw): 가장 기본적인 스위치 입니다.
- SPDT (Single Pole, Double Throw): 3로 스위치로 불리기도 합니다.
- DPST (Double Pole, Single Throw): 누전차단기나 배선용 차단기 등의 스위치에 입니다.
- DPDT (Double Pole, Double Throw): 모터의 회전방향을 바꾸거나 2개의 모선 중에 1개의 모선을 골라서 전등을 켤 때도 사용됩니다.
pole은 극 수를 나타내고, throw는 on-off되는 라인의 수를 이야기 합니다.
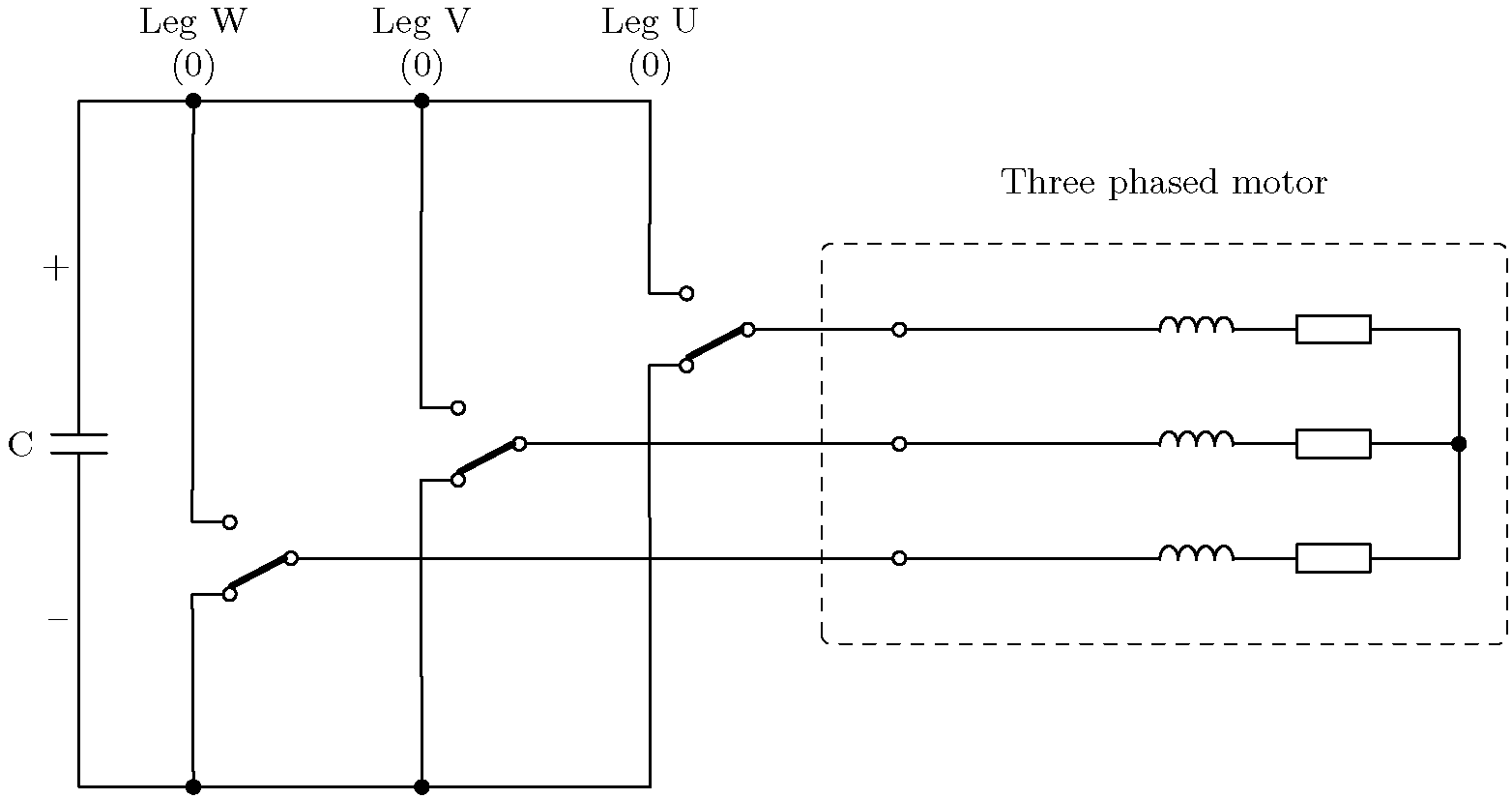
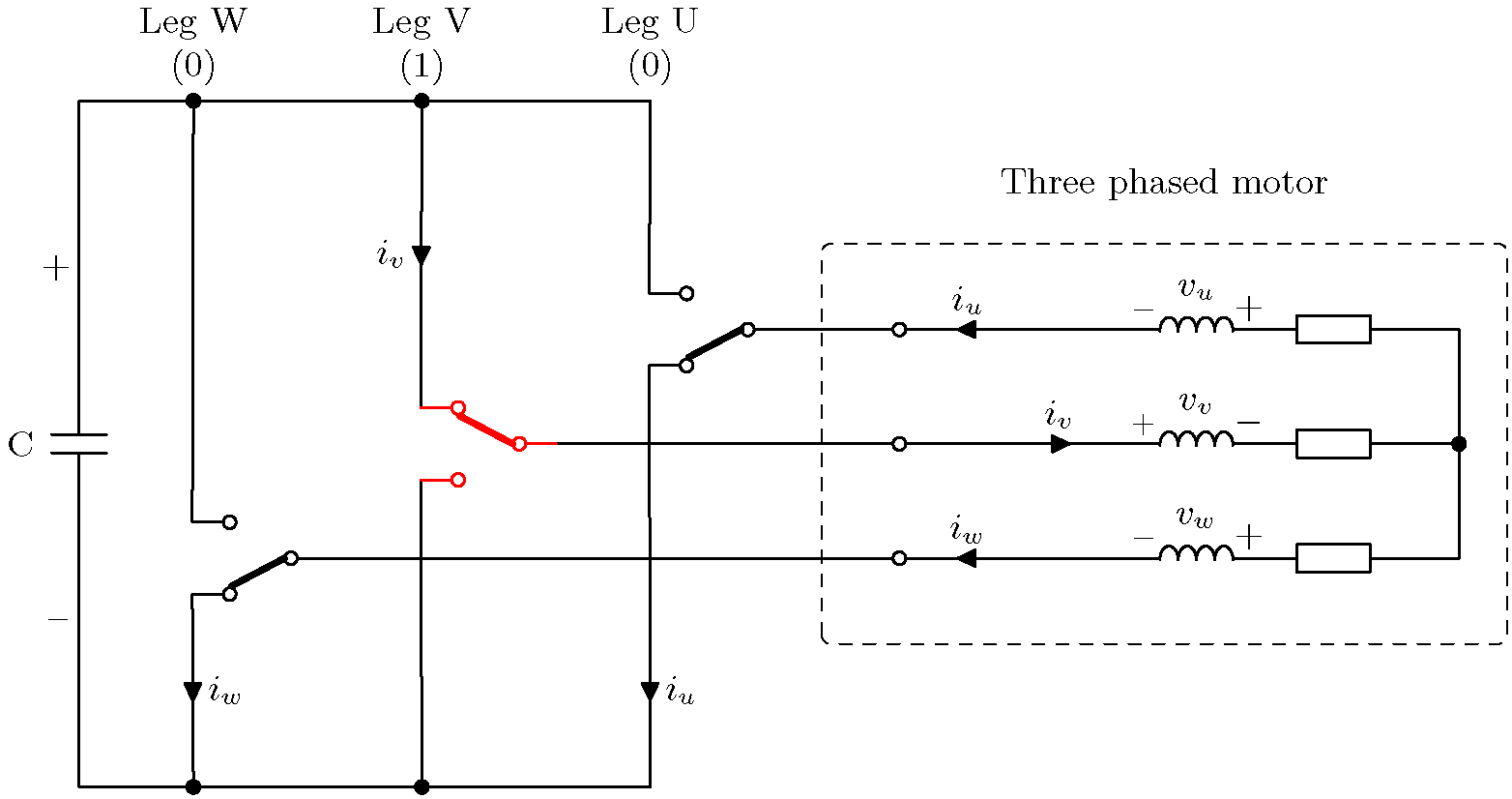
위의 예는 가장 왼쪽의 레그(W)가 위쪽 트랜지스터를 닫고 아래쪽 트랜지스터를 여는 트랜지스터 조합을 보여줍니다. 다른 두 레그(V와 U)는 위쪽 트랜지스터를 열고 아래쪽 트랜지스터를 닫습니다. 이는 W상에 양의 전압을 적용하는 반면 다른 두 상은 음의 전압을 적용하는 것과 같습니다. 전류 화살표는 양의 DC 링크에서 음의 DC 링크로의 전류 경로를 보여줍니다.

단순화된 회로도에서 이제 각각 두 개의 다른 위치에 있을 수 있는 세 개의 스위치가 있음을 알 수 있습니다. 따라서 가능한 스위치 구성의 총 수는 다음과 같습니다 .2 ^ 3 = 8.
이러한 구성 중 여섯 가지(V1~V6)는 연결된 모터에 적용되는 다른 전압에 해당하며 지금부터 기본 벡터 라고 합니다. 마지막 두 가지(V0=000, V7=111)는 단자에서 0볼트를 나타내므로 0 벡터 라고 합니다 .
U-상은 일반적으로 0°에서 기본 벡터 각도의 기초를 형성합니다. 각도의 원점은 스테이터 내부의 권선 물리적 위치입니다. 원주 주위에 120° 간격으로 설치됩니다. 각 권선은 양전압과 음전압을 가질 수 있으므로 180° 분리에서 두 각도를 차지합니다. 예를 들어 240°와 60°는 각각 양과 음의 상태에서 W-상입니다.
이진법에서 이러한 벡터 조합은 8개의 서로 다른 이진 값으로 표현될 수 있으며 여기서는 다음과 같이 명명됩니다. V0 ~ V7:
000 - v0 (zero vector)
001 - v1 (Phase +U)
010 - v2 (Phase +V)
011 - v3 (Phase -W)
100 - v4 (Phase +W)
101 - v5 (Phase -V)
110 - v6 (Phase -U)
111 - v7 (zero vector)
3개의 이진 숫자는 각각 하나의 브리지 다리를 나타내며, 값 1은 위쪽 트랜지스터가 닫혔음을 나타내고 값 0은 아래쪽 트랜지스터가 닫혔음을 나타냅니다.
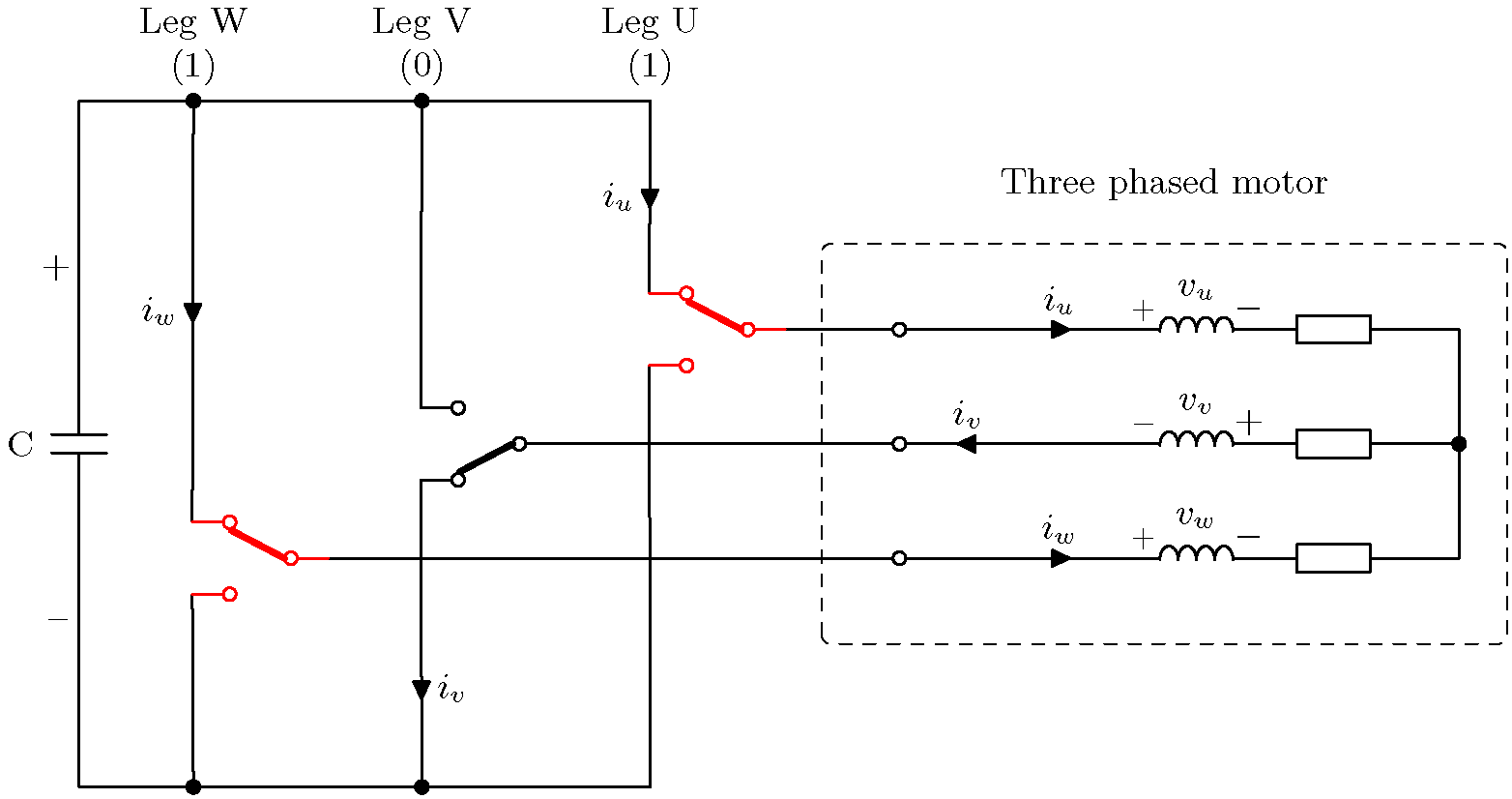
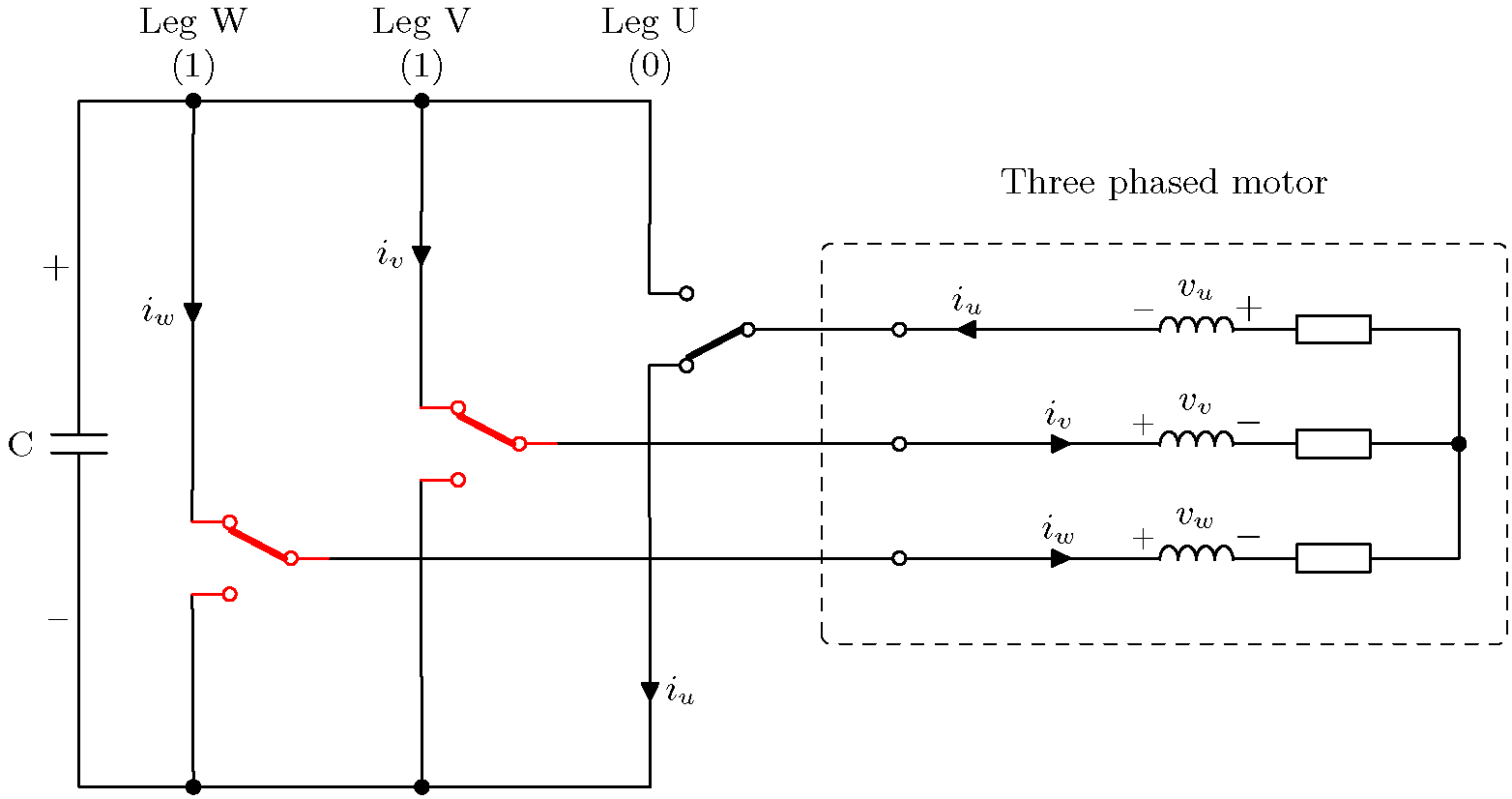
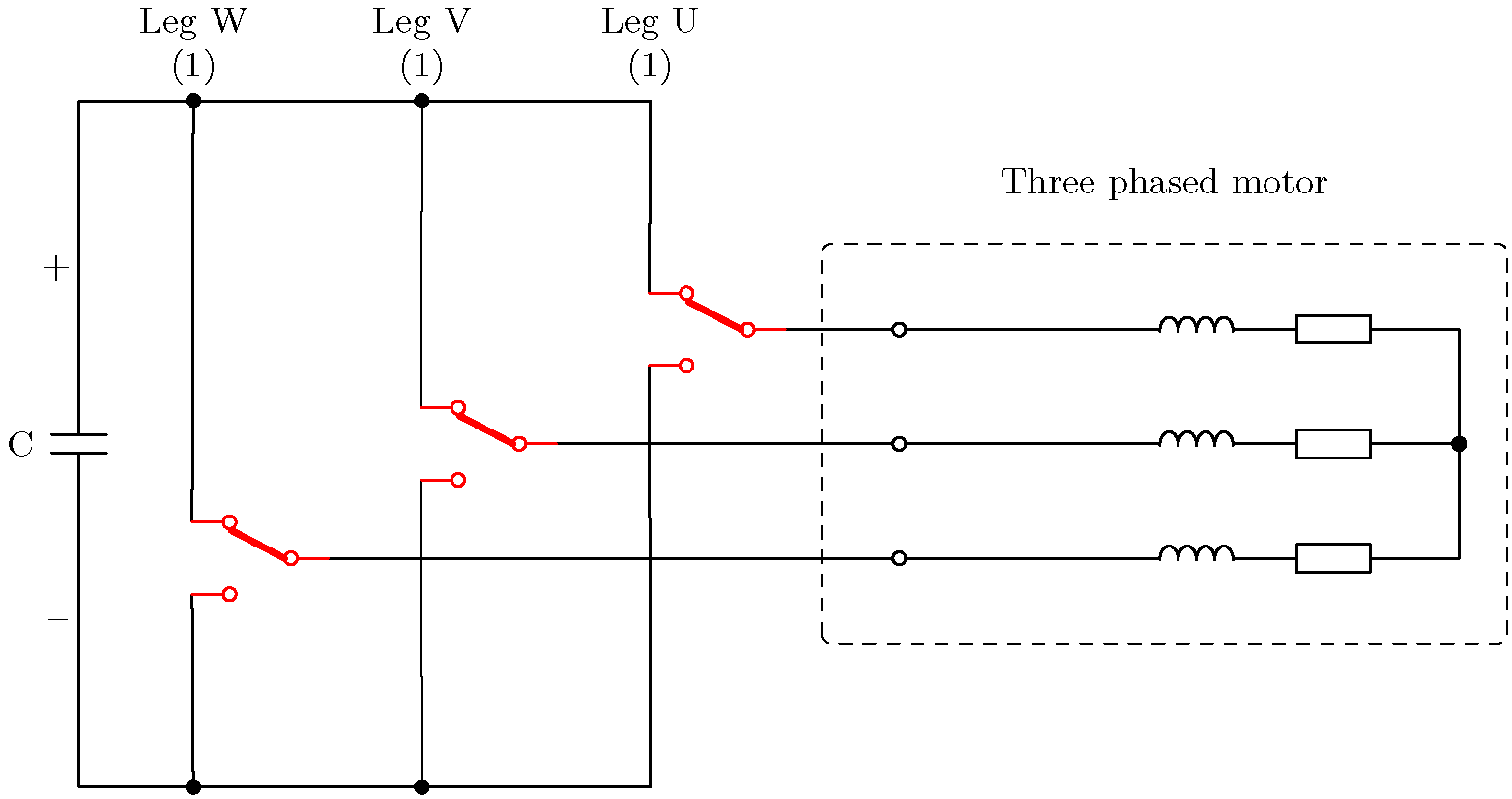
모든 8가지 조합과 그에 따른 모터 전압 및 전류 방향이 아래에 나와 있습니다.
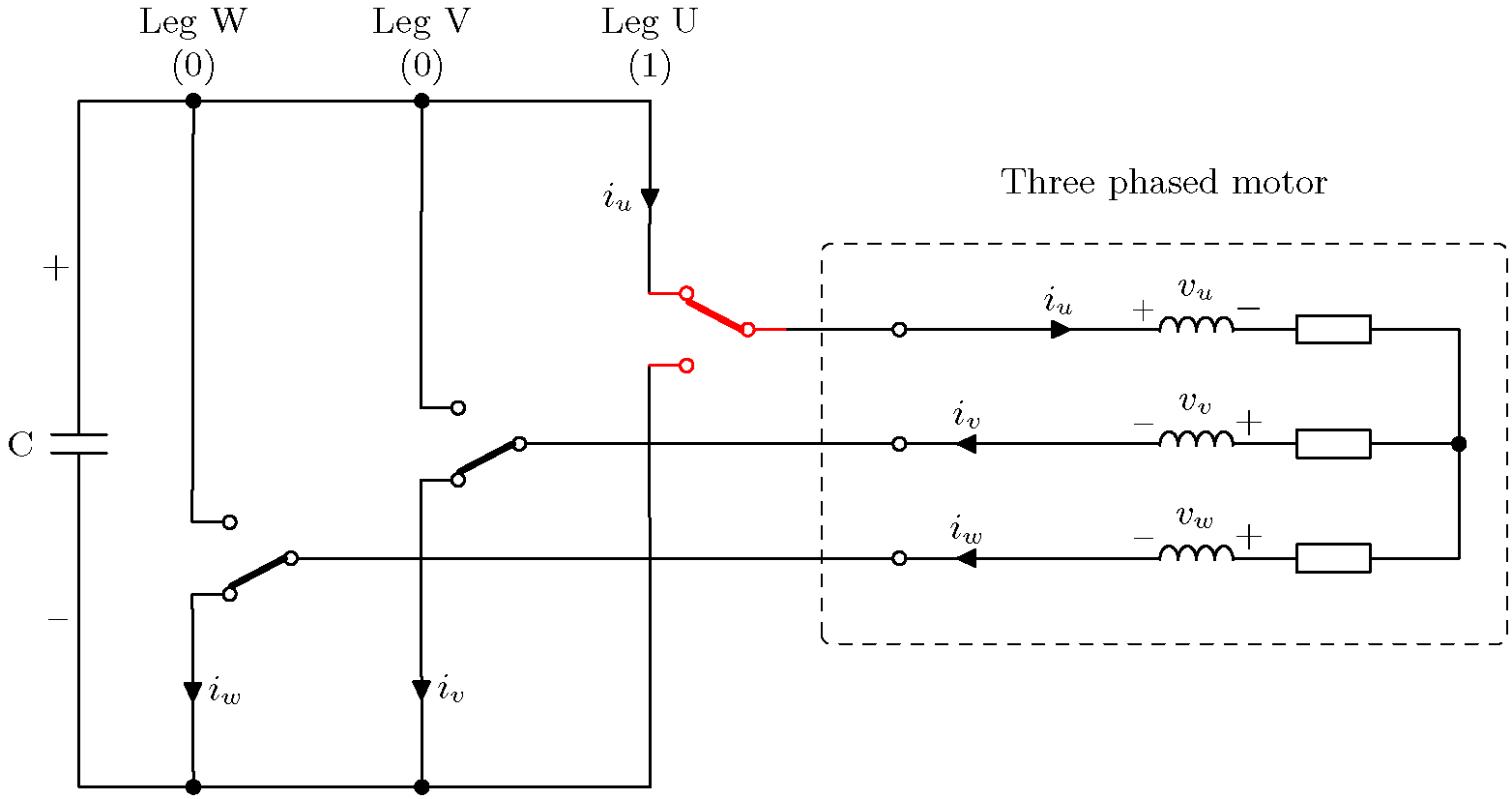


4. 출력 전압 합성
지금까지는 컨버터가 DC 링크 전압을 단자에 출력할 수 있다는 것과 사용 가능한 6개의 벡터 각각이 모터의 전류 및 전압 방향에 어떻게 영향을 미치는지 보여주었습니다.
이 섹션 에서는 인접한 전압 벡터와 켜짐 및 꺼짐 시간의 타이밍을 빠르게 번갈아가며 모든 전압 벡터를 합성하는 방법을 보여줍니다 .
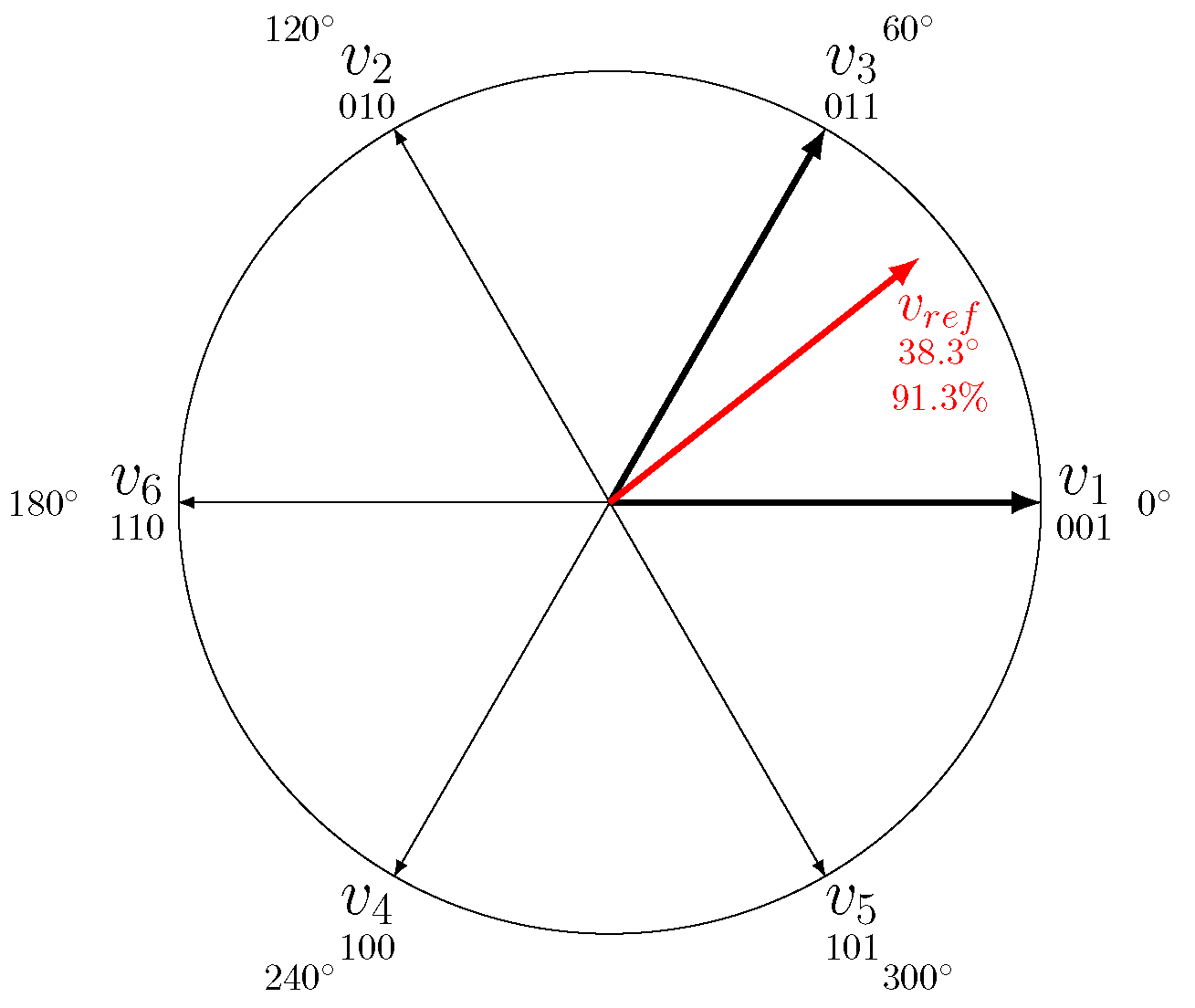
위 그림에서는 인버터가 사용 가능한 기본 벡터를 사용하여 합성해야 하는 참조 벡터의 예가 나와 있습니다.
그림에서 보면 참조 벡터(Vref, 38.3∘ )가 V1 과 V3 사이에 위치하는 것을 알 수 있습니다. 이 섹터를 섹터 1이라고 합니다.
이제 이 두 기본 벡터 사이를 빠르게 번갈아가며 전압 벡터를 에뮬레이션할 수 있습니다..
두 개의 0 벡터 V0 와 V7 도, 스위칭 패턴에 데드 타임을 추가하는 데에 사용됩니다. 이 데드 타임은 전압 크기를 줄일때, 즉 전압 기준 크기가 100% 미만일 때 필요합니다.
실제 합성은 삼각파의 트리거를 사용하여 만들 수 있습니다. 먼저, 사용 가능한 필요한 기준 전압 이 이미 있다고 가정합니다. 예를 들어, dq 변환 ( https://bahk33.tistory.com/218 ) 에 설명된 역 Clarke/Park 변환을 통해 계산됩니다 .
아래 그림은 삼각파를 통해 원하는 전압이 3개의 인버터 레그 각각에 대한 바이너리 온/오프 신호로 변환되는 방식을 보여줍니다. 여섯 가지 다른 예가 표시되어 있으며, 각각 다른 섹터에서 다른 각도를 갖습니다.
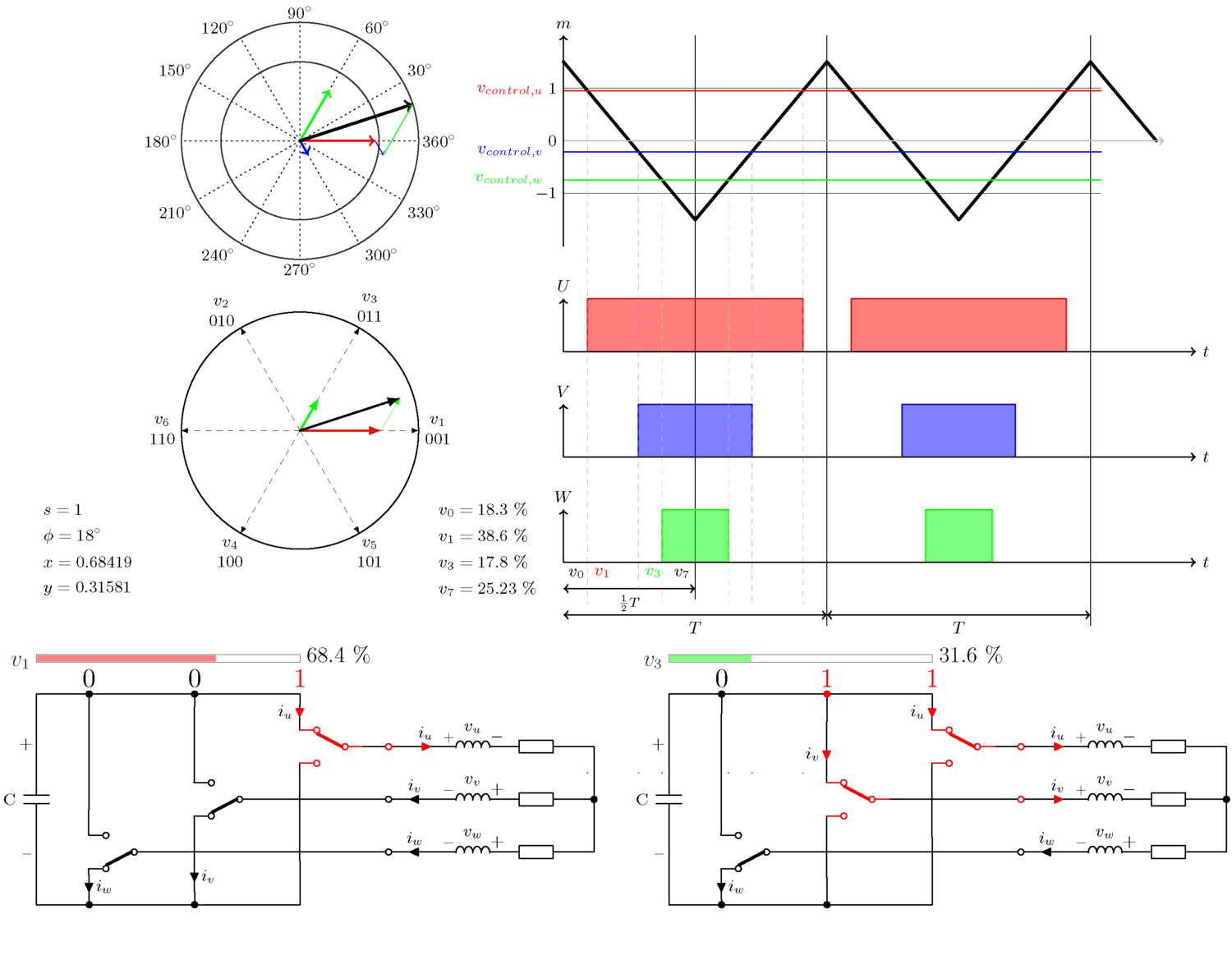
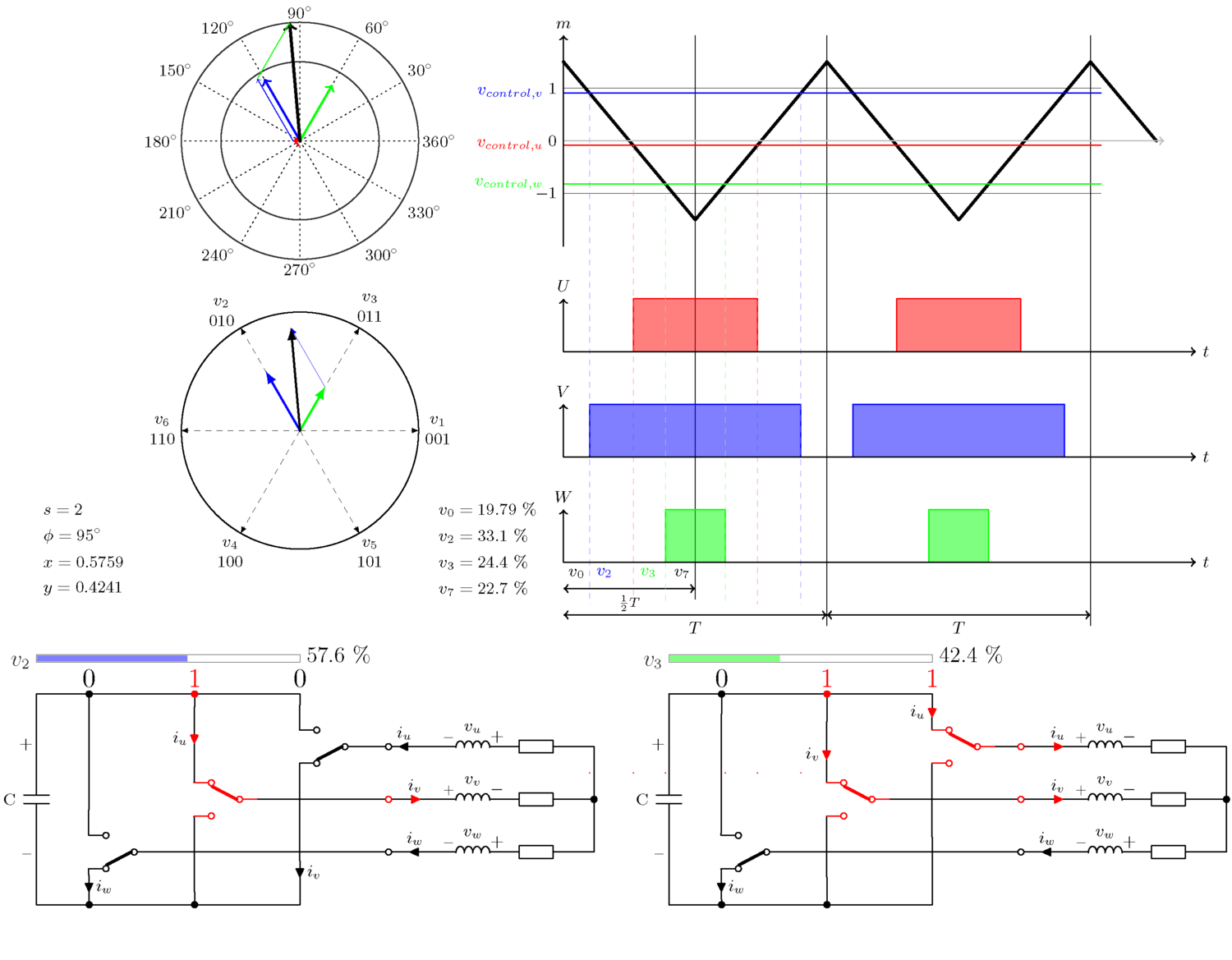
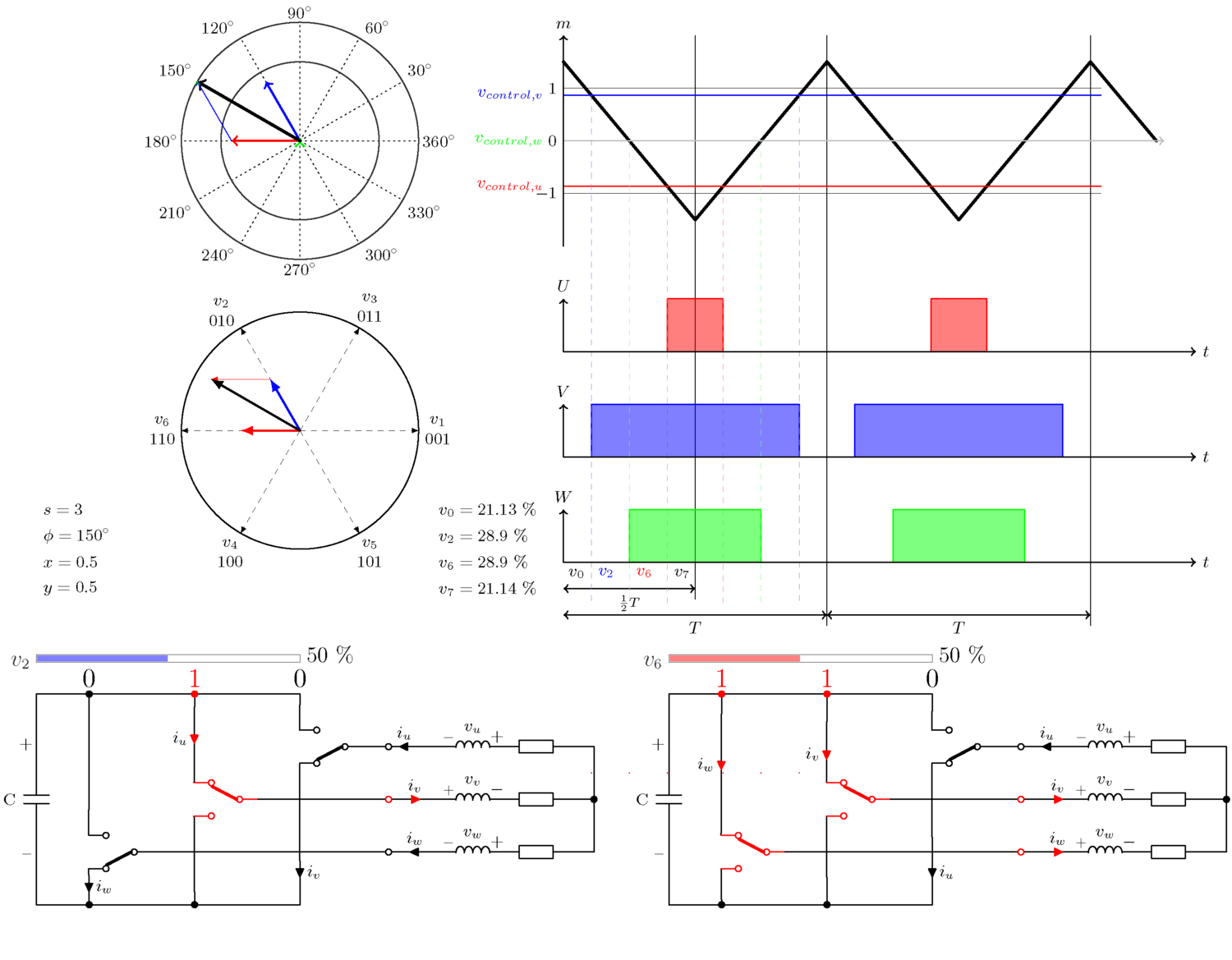

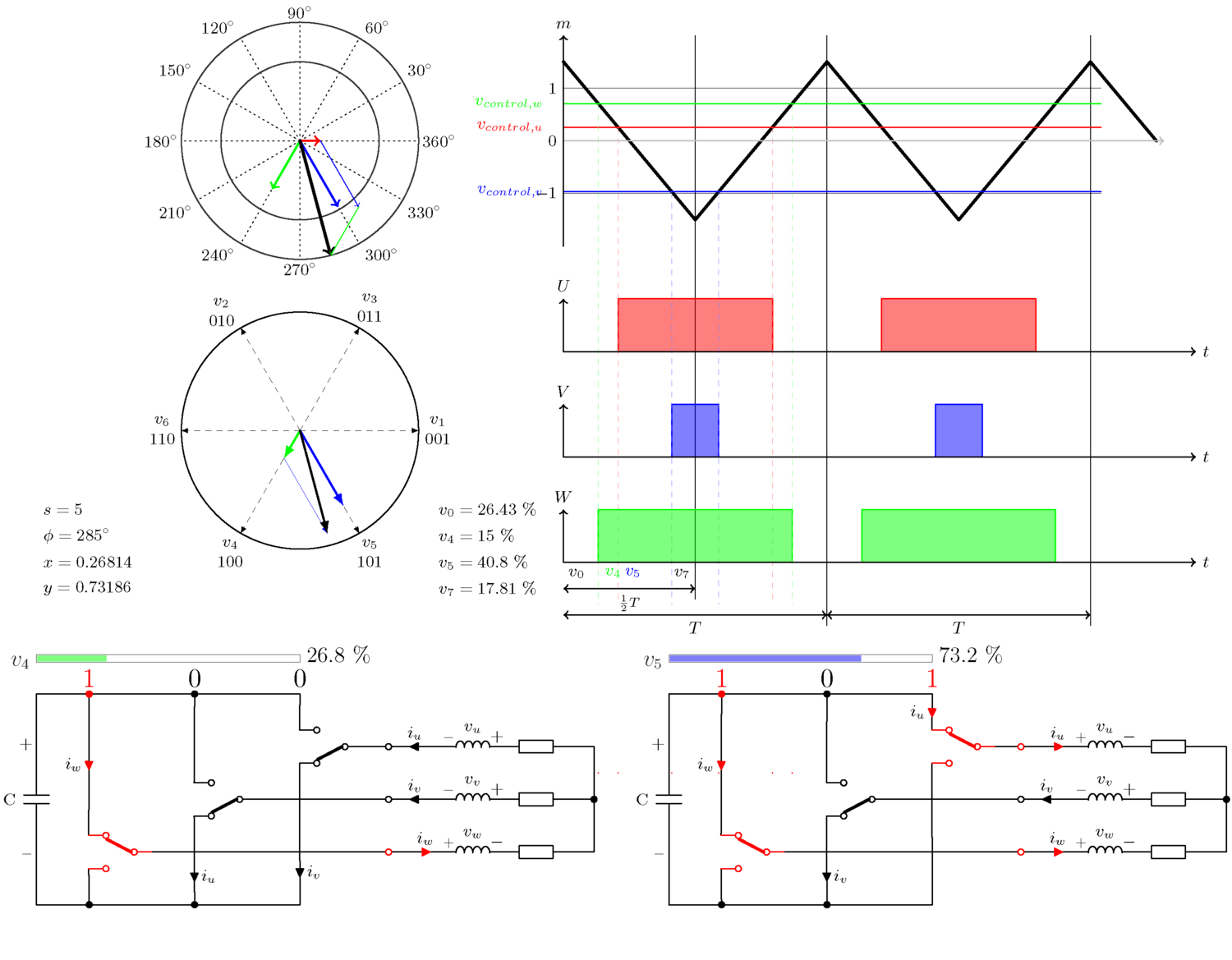
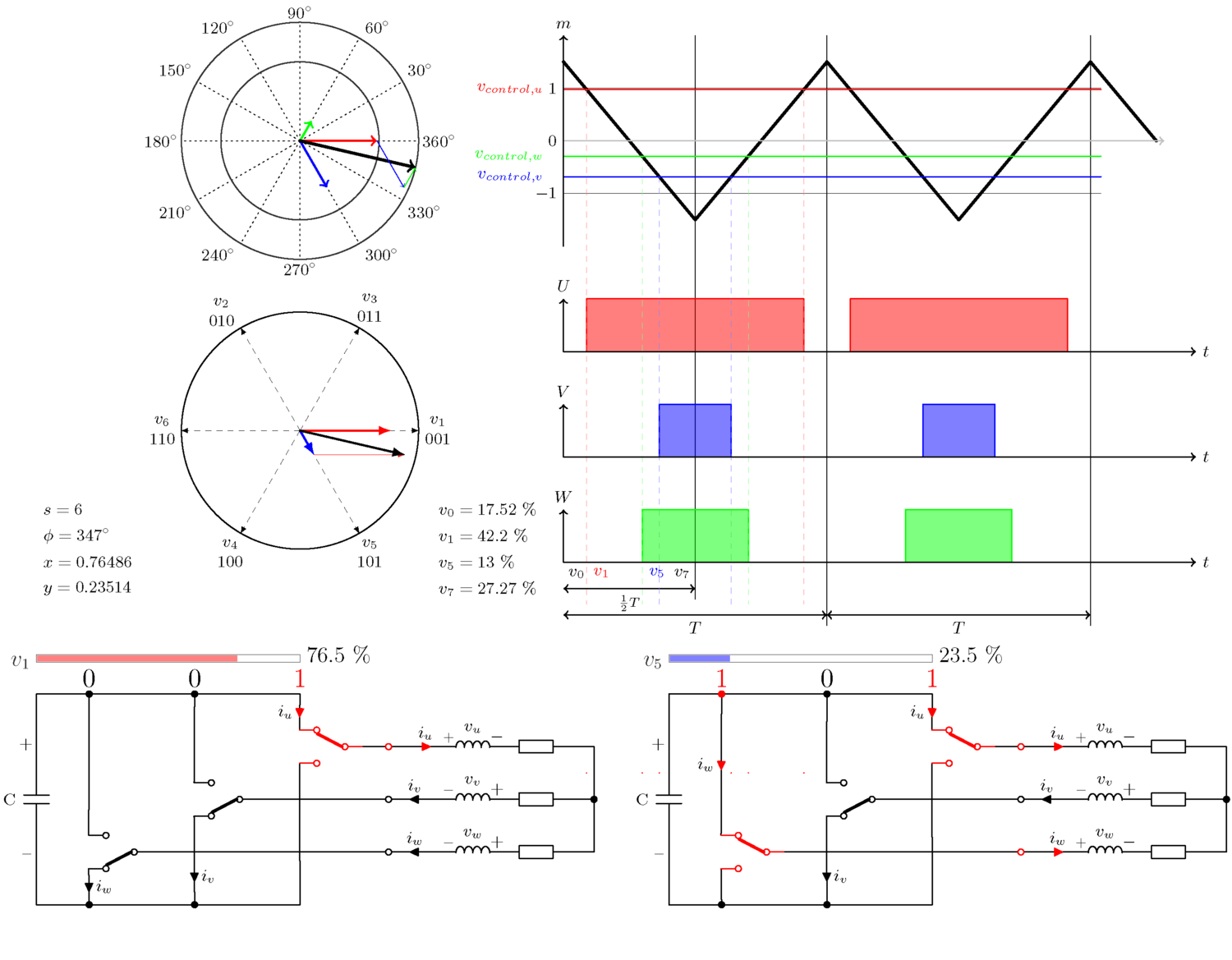
5. 개념 설명
여기서 잠시 숨을 고르지요. 이 그림에는 많은 정보가 들어 있고, 그 중 다른 부분을 더 잘 설명하기 위해, 아래에서 설명할 네 개의 다른 영역을 골랐읍니다.
1) - 삼각파에 대한 입력 및 투영:
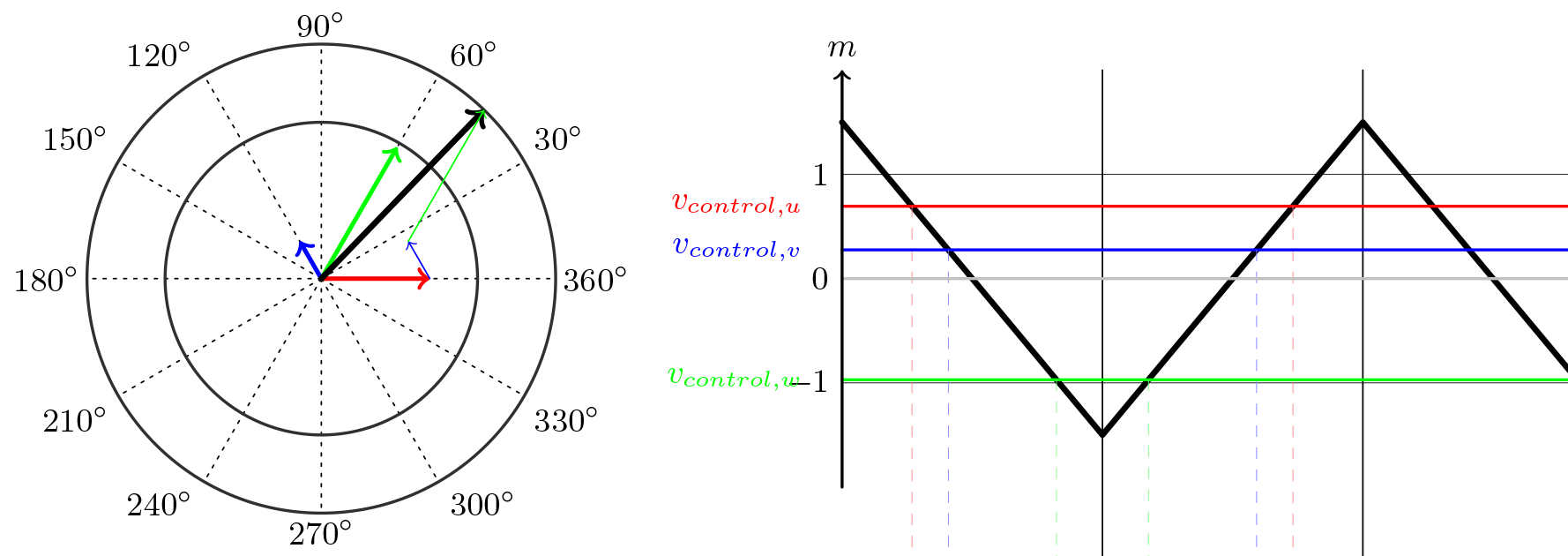
위 원은 "입력" 또는 "기준"입니다. 어떤 사람들은 이것을 주문 신호라고도 부릅니다. 이것이 우리가 이루고자 하는 것입니다. 서로 다른 각도의 세 가지 다른 전압이 함께 하나의 크기와 하나의 각도를 갖는 공간 벡터를 형성합니다.
보시다시피 U-위상(빨간색)은 최대 양의 값에 가깝습니다. 이 수준은 또한 원 오른쪽의 그래프에 여기서 제어 전압이라고 하는 삼각파와 함께 표시되어 있으며,. 이 삼각 파형의 주파수는 공간 벡터의 주파수보다 몇 배 더 높습니다. 일반적으로 1~20kHz이지만 수백 헤르츠 또는 최대 수백 킬로헤르츠의 응용 프로그램도 많이 있읍니다.
W상(녹색)은 최대 음수값에 가깝고 V상(파란색)은 양의 방향으로 0에서 뻗어나갑니다.
이 세 가지 값이 삼각파와 교차하는 방식은 어떤 스위치를 닫을지, 그리고 얼마나 오랫동안 닫은 상태를 유지할지에 대한 직접적인 영향을 미칩니다.
2) - 입력을 상태 전환으로 변환:
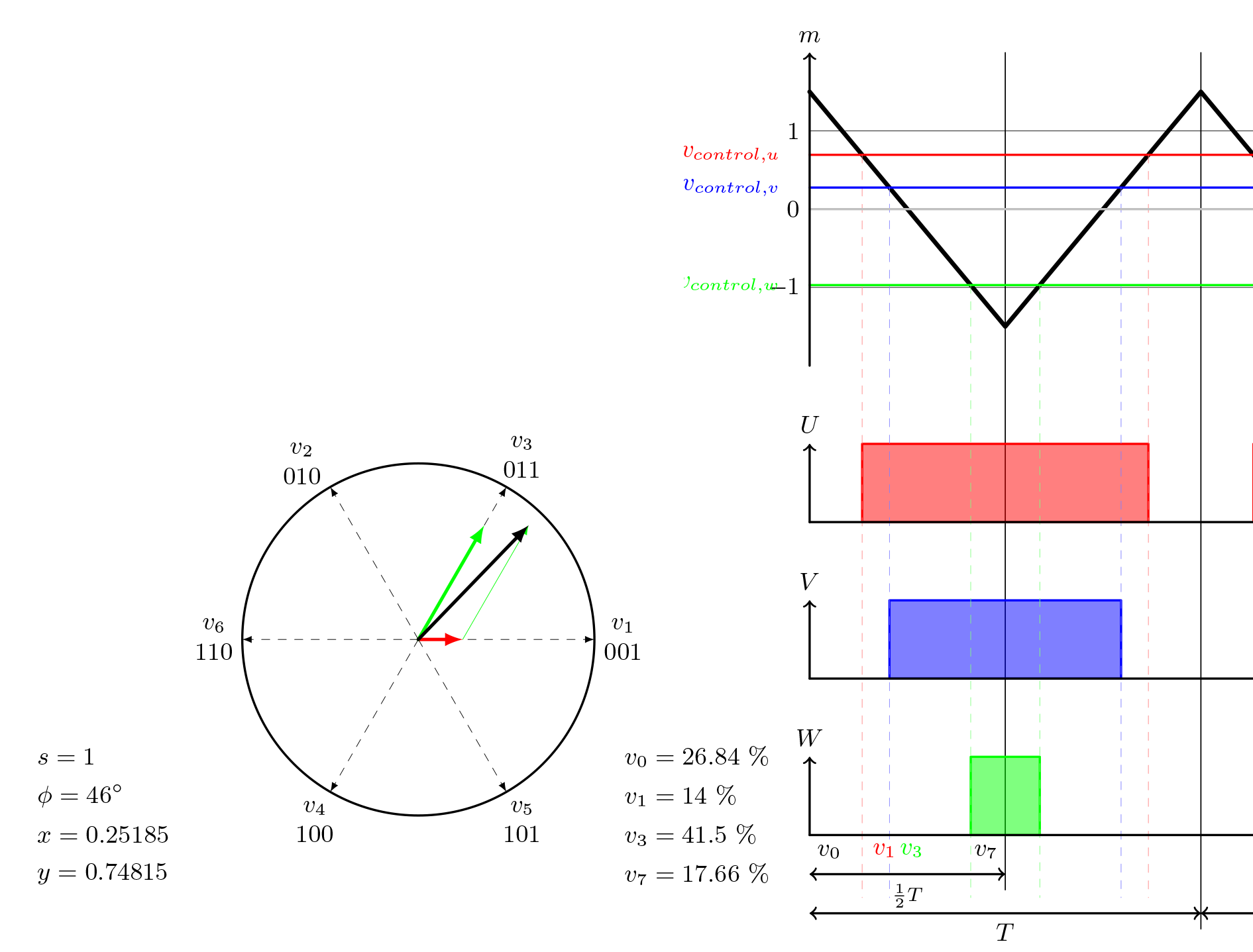
그림의 오른쪽 부분을 보세요.
이 부분의 주요 초점은 삼각파에서 아래로 튀어나온 점선입니다. 이는 제어 전압이 삼각파와 교차하는 곳에서 시작됩니다. W축 바로 아래, 1/2 T 화살표 바로 위에 , 항상 4개의 다른 섹션이 보입니다. 위 그림에서는 v0, v1, v3, v7 입니다. 다른 공간 벡터 각도와 크기의 경우, 이 네 섹션의 너비는 바뀌지만, 전체 너비는 항상 동일합니다.
이 예의 각도(46°)에서 첫 번째 점선은 빨간색 선입니다. 세 축의 시작과 빨간색 점선 사이에는 활성 전압 벡터가 없습니다. 이 영역의 세 가지 제어 전압은 모두 삼각파 아래에 있습니다. 즉, 모든 스위치가 꺼져 있습니다. 000 - 제로 벡터 v0.
다음 섹션; 빨간색과 파란색 점선 사이. U-위상 제어 전압은 이제 트리거 라인 위에 있고 다른 두 개는 여전히 아래에 있습니다. 이렇게 하면 U-스위치가 활성화됩니다 . 001 - 섹터 v1.
세 번째 섹션: 파란색과 녹색 선 사이. 이제 U와 V가 모두 활성화되었습니다. 011 - v3.
마지막 섹션: 세 개의 스위치가 모두 활성화되었습니다. 이것은 111입니다. v7 - 두 번째 영벡터.
모든 각도와 크기에서 동일한 패턴이 보일 것입니다. 제로 벡터 - 기본 벡터 - 기본 벡터 - 제로 벡터. 가 반복합니다. 유일하게 변하는 것은 이러한 섹터의 폭 (즉, 정시)과 여섯 가지 기본 벡터 중 어떤 것을 사용하는지입니다.
W축의 왼쪽에는 정시 백분율도 표시됩니다. 원하는 진폭이 낮으면 제로 벡터는 정시가 증가하고 진폭이 높으면 그 반대가 됩니다. 이는 변조 지수( modulation index ) 라는 스케일링 계수에 의해 제어됩니다 . 원하는 진폭이 삼각파보다 높으면 과변조 ( over modulation ) 라는 현상이 발생합니다. 이는 나중에 설명합니다.
3) - 벡터 그림
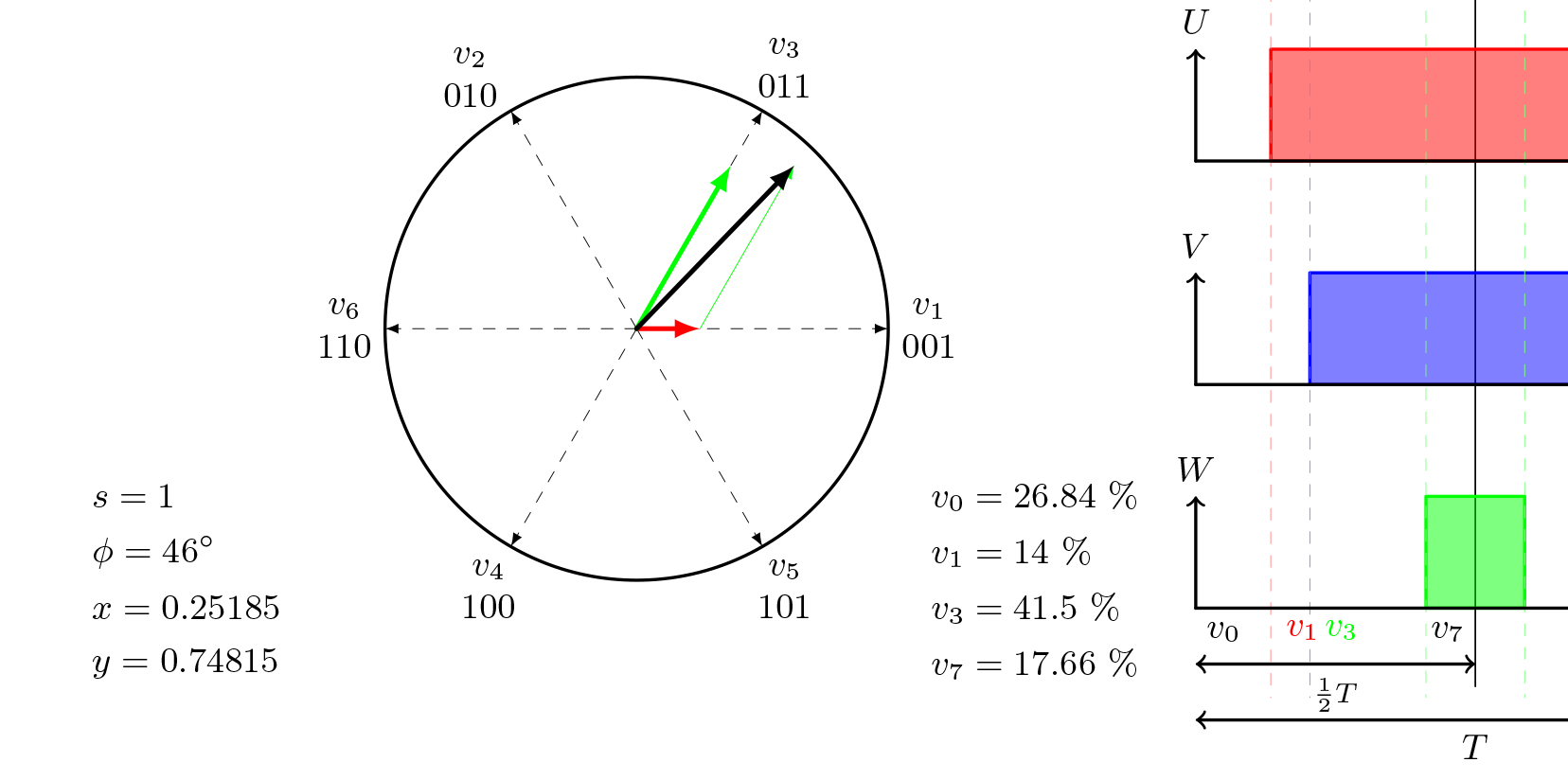
이제 우리는 우리가 번갈아가야 할 두 벡터가 무엇인지 알고 있습니다.v1 과 v3 입니다.
켜짐 시간을 올바르게 맞추면 입력 전압 공간 벡터와 동일한 각도에서 전압 벡터를 에뮬레이션하게 됩니다.
녹색 v3-벡터는 W축 아래의 원 벡터 다이어그램과 "섹터 다이어그램"에서 모두 최대값에 가깝습니다. 마찬가지로 v1 벡터는 최소값에 가까운 벡터입니다.
공간 벡터 원( space vector circle ) 안의 얇은 녹색 선은 이 두 기본 벡터가 실제로 벡터 합으로 원하는 공간 벡터를 형성한다는 것을 보여주기 위한 시각적 보조 도구 입니다.
그림의 왼쪽 값은 현재 벡터가 있는 섹터(s), 각도(pie) 및 x그리고y 는 가중치를 보여줍니다. 두 기본 벡터 각각에 대해. 나중에 다시 다룰게요.
4) - 두 개의 교대 스위칭 구성의 그림
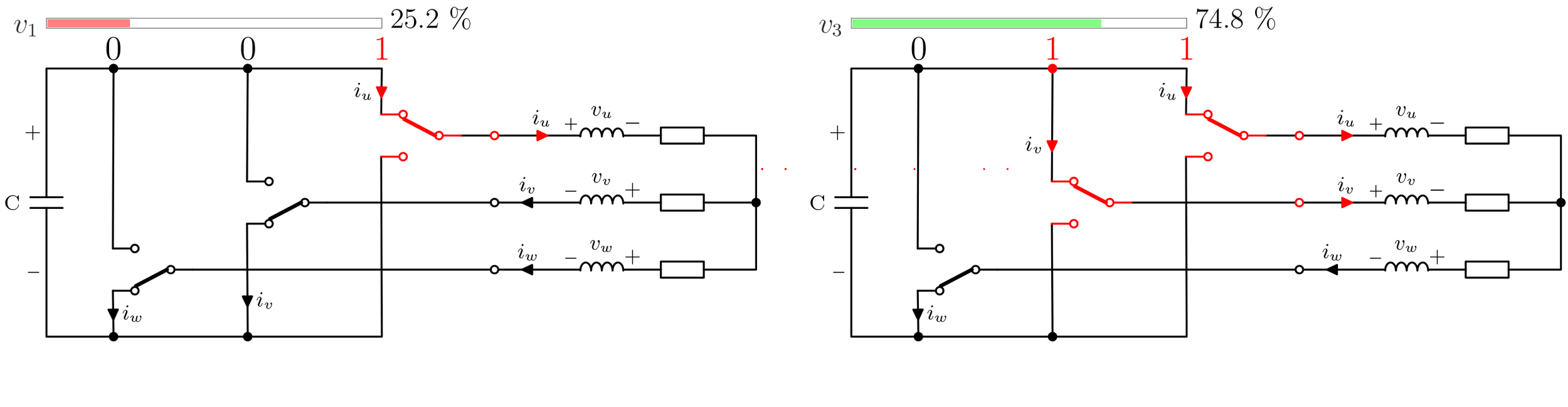
드라이브가 번갈아 가며 사용할 두 가지 다른 스위칭 조합(기본 벡터)이 여기에 표시됩니다. 각 구성 위의 진행률 표시줄은 두 기본 벡터의 총 켜짐 시간과 비교하여 켜진 시간을 나타냅니다. 즉, 서로에 대한 켜짐 시간입니다.
추가로 제로 벡터가 제공되며, 이는 전압 레벨이 낮아질수록 증가합니다.
두 개의 사인파가 90도 떨어져 있는 것처럼 서로 반대 "위상"에 있다는 점에 주의하세요. 왼쪽 구성이 주기를 완료하면 오른쪽 구성은 절반이 됩니다.
이 스위칭 방식은 또한 멋진 기능을 사용합니다. 한 번에 하나의 스위치만 상태를 변경합니다. 이는 기계의 고조파를 줄이고 스위칭 손실도 줄이는데, 이는 모든 유형의 전력 전자 장치를 설계할 때 고려해야 할 매우 중요한 측면입니다.
5) 요약
그림에서 가장 중요한 부분은 가장 낮은 축(W) 아래의 영역입니다. 각 기본 벡터가 각 기간 동안 활성화된 부분을 보여줍니다.티티백분율 숫자는 해당 축의 왼쪽에 표시됩니다.
또한 모든 패턴이 0 벡터로 시작하고 끝나며, 모든 전환 사이에 단 하나의 스위치만 변경된다는 것을 알 수 있습니다. 이는 과열 및 토크 변동을 유발하는 모터의 고조파를 크게 줄입니다. 또한 토크에 기여하지 않거나 필요한 자기장을 유지하는 데 필요한 전류는 원치 않습니다. 이는 전력 전자 부품의 손실이 전류에 따라 달라지고 냉각 시스템에 스트레스를 주는 열로 변환되기 때문입니다. 트랜지스터와 다이오드의 과열은 오늘날 전력 전자 장치를 설계할 때의 주요 과제 중 하나입니다. 대안은 더 높은 전류 정격의 컨버터를 설계하는 것이지만, 이렇게 하면 가격이 상승합니다.
또한, 위 그림의 하단에 두 개의 도식이 표시됩니다. 이는 현재 섹션에서 사용 중인 두 개의 기본 벡터에 대한 스위치 상태를 나타냅니다. 위의 백분율 표시는 다른 것에 대한 온타임을 나타냅니다. 예를 들어, 각도가 정확히 두 개의 기본 벡터(예: 30°) 사이인 경우 두 기본 벡터는 각각 50%의 시간 동안 켜집니다. 이 백분율은 기간에 대한 총 온타임( T )을 나타내지 않는다는 점에 유의하세요. . 전압 크기가 최대값보다 작으면 전압을 평균화하기 위해 제로 벡터가 추가됩니다. 따라서 전압 크기가 70%이고 여전히 30°일 때 각 기본 벡터의 ON 시간은 서로에 대해 여전히 50%이지만 전체적으로 이 기간 내에 30%의 제로 벡터링이 발생합니다. 따라서 각 트랜지스터의 실제 온 시간은 35%가 됩니다.
T= Tv1 + Tv3 + Tv0 + Tv7 = 35% + 35% + 15% + 15% = 100%
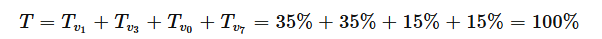
전체 애니메이션은 아래와 같습니다.
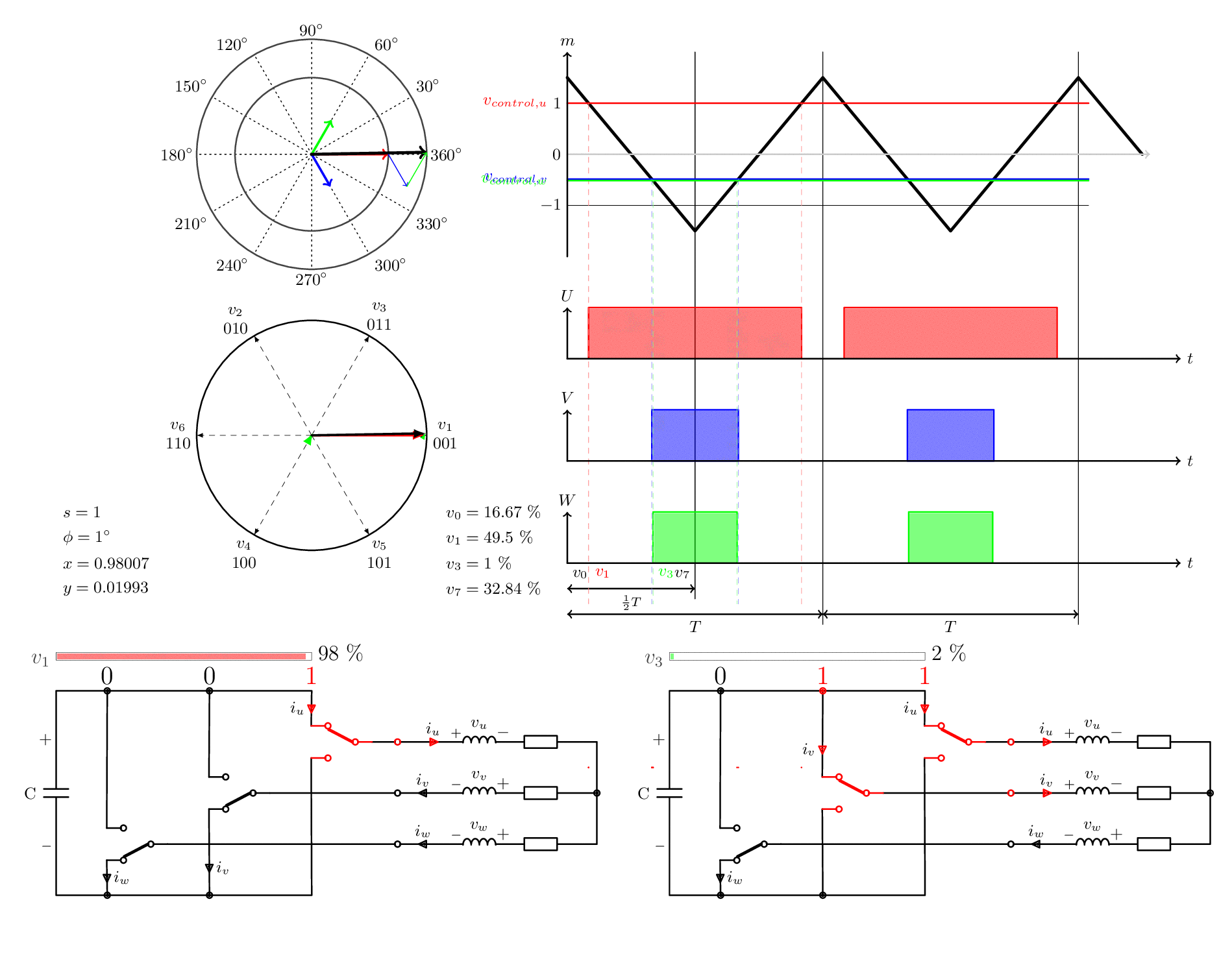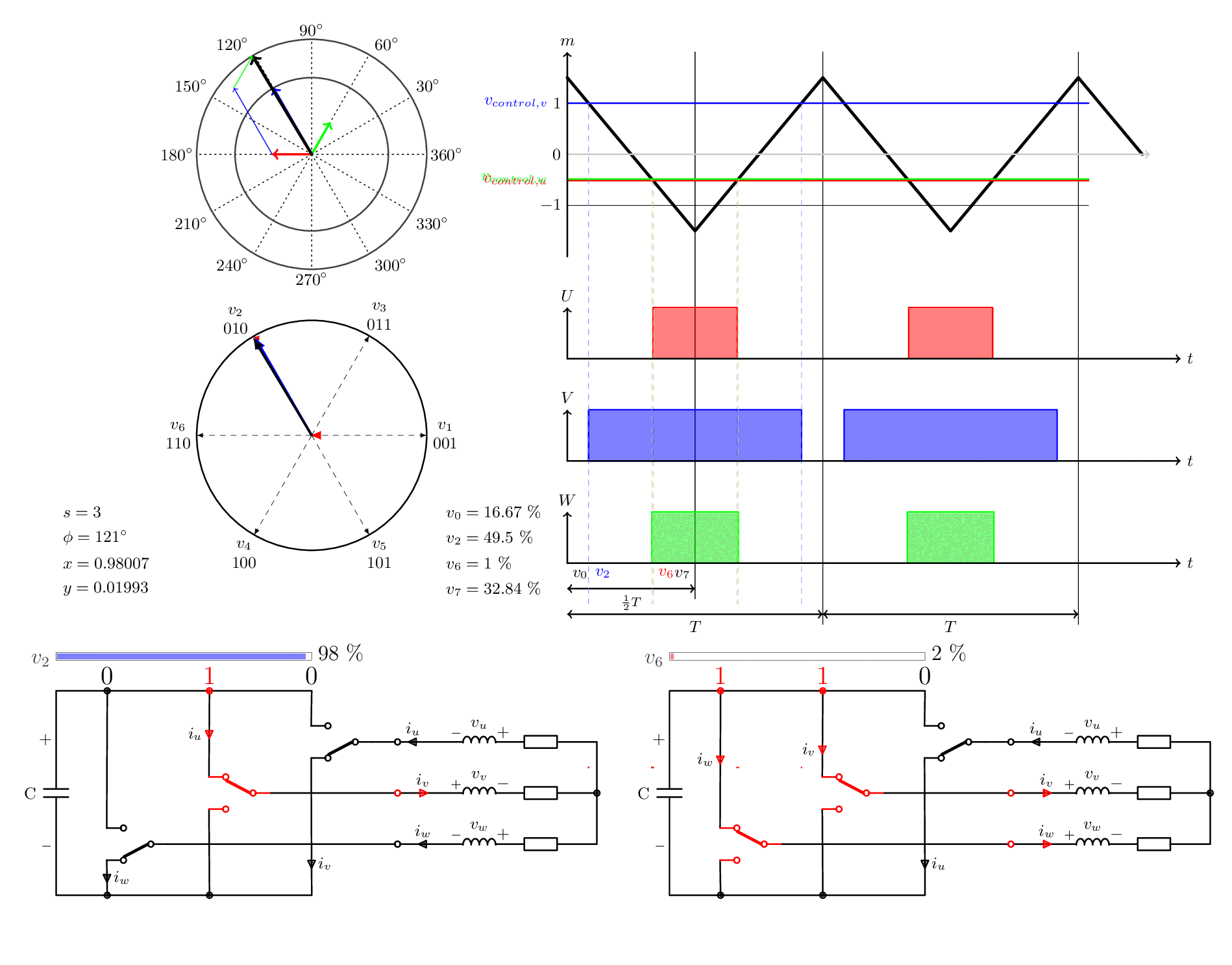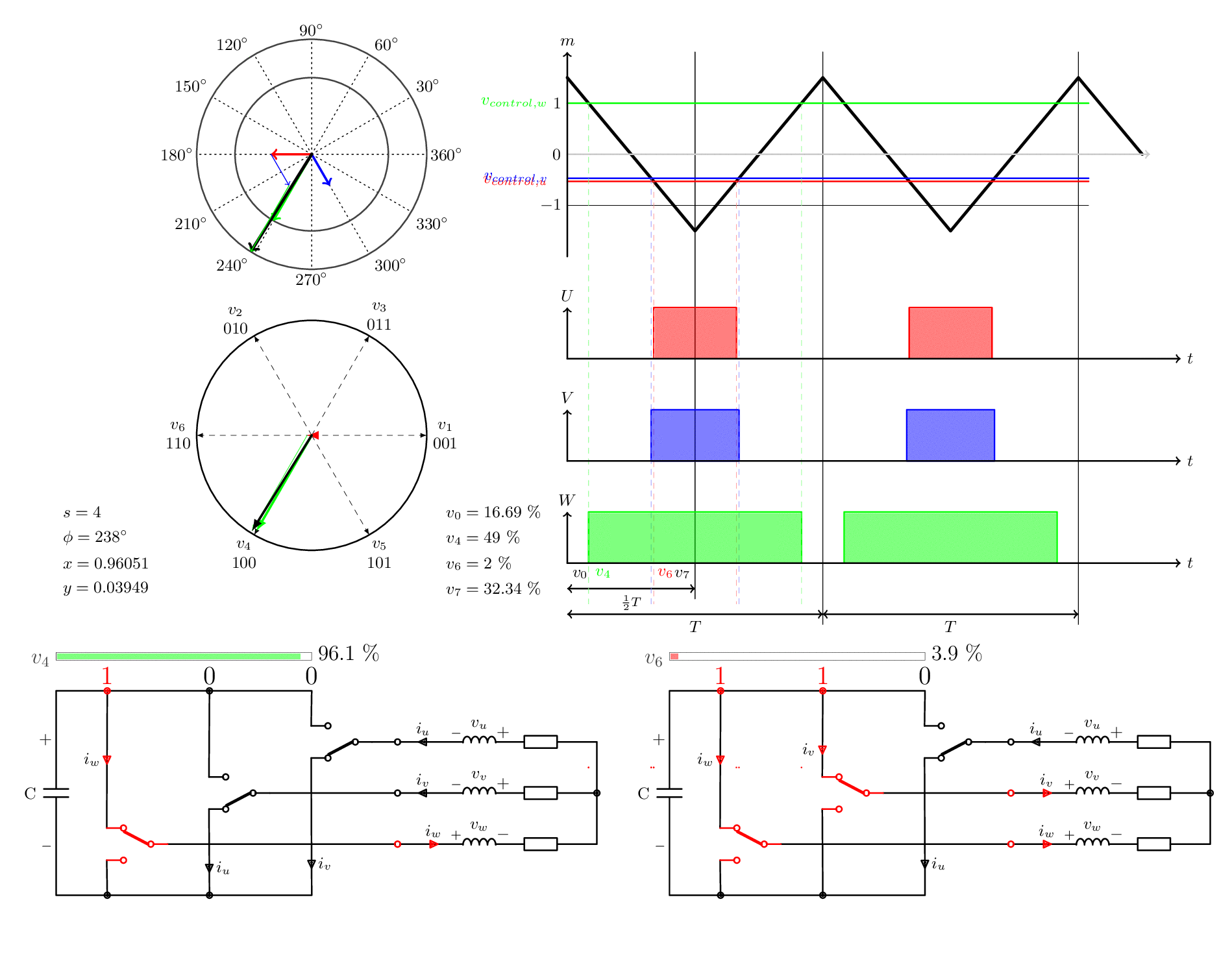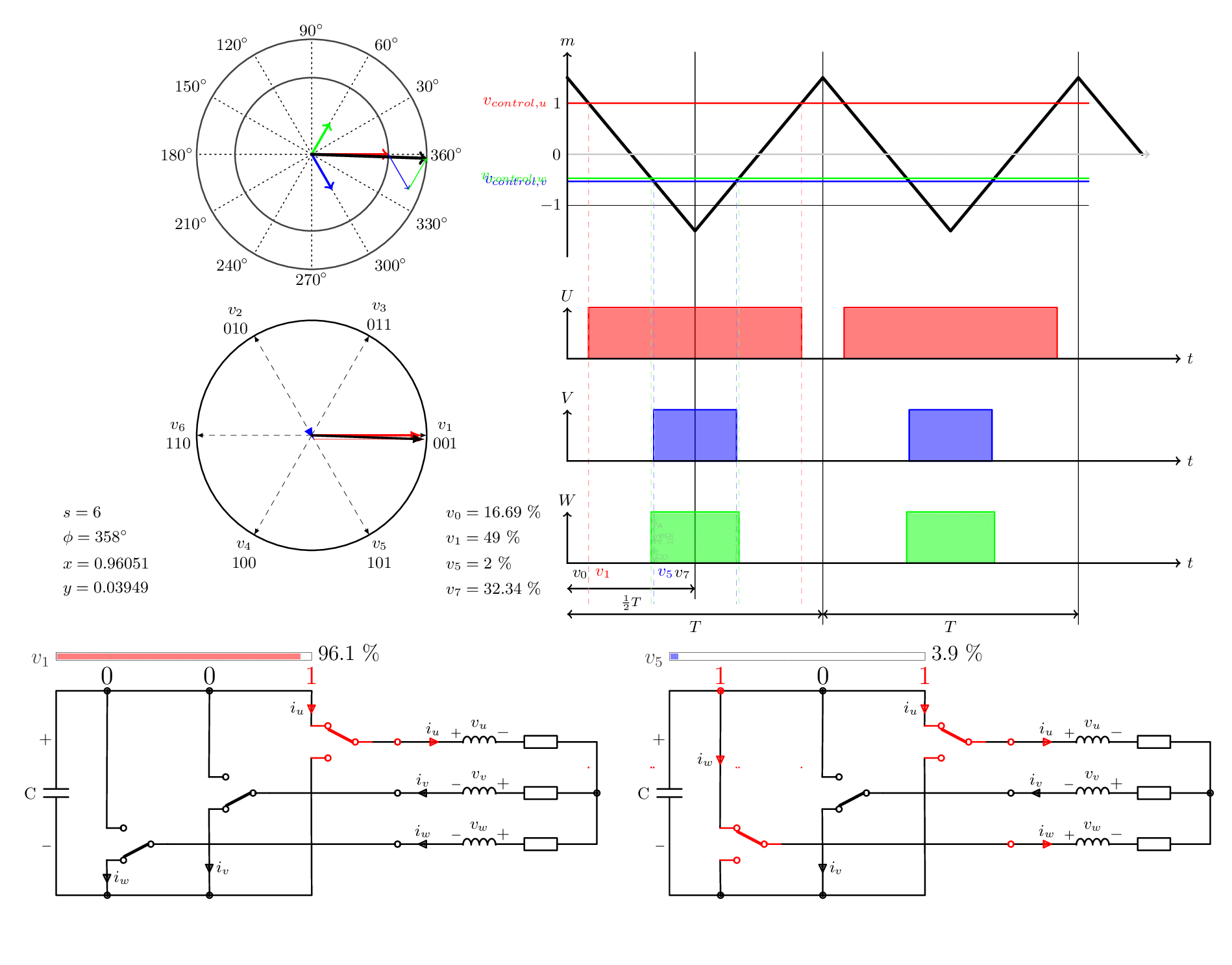
6) 자세한 예
문제:
- 드라이브가 38.3° 각도에서 630V의 전압 벡터를 변조해야 한다고 가정 한다면.

아래첨자 s 가 있는 곳 스테이터 프레임 참조(즉, 로터가 아님)를 나타내고 상위 첨자( u ) 는각도 기준(0°)이 위상 U(0°)에 있음을 나타냅니다.
- 38.3°는 기본 벡터 1(0°)과 3(60°) 사이에 있으므로, 우리가 활용할 두 가지는 바로 이 두 개입니다.
- 각 기본 벡터를 얼마나 사용하는지 결정하는 방정식은 다음과 같이 작성할 수 있습니다.

v1 과 v3 사용되는 두 가지 기본 벡터입니다. x그리고 y 를 각 벡터 v1 과 v3 에 대한 알려지지 않은 미지수라 하고, 가중치 요소 입니다 .
- DC 링크 전압은 975V이고 모터 정격 단자 전압은 690V입니다(해양 산업의 일반적인 값)
먼저, 실제 구성 요소가 설정됩니다.
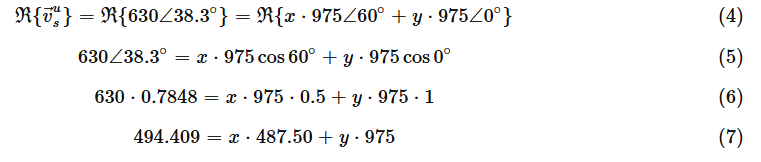
두 번째로, 우리는 허수 성분을 설정합니다.
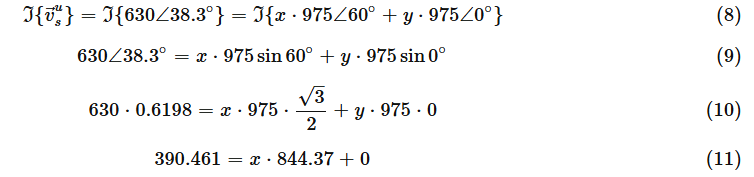
방정식을 7 그리고11 을 서로 적용하며는, 이제 우리는 x,y 를 찾을 수 있습니다 먼저 식 11에서

y 를 구하기 위하여 - 방정식 7 에 x 값을 넣으면:

찾은 값을 삽입하여 결과를 다시 확인해 보겠습니다.
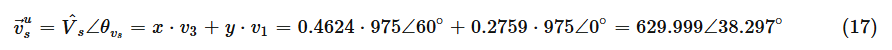
이 결과는 38.3° 각도에서 630V였던 원래 목표에 매우 가깝습니다.
7) 그러면 출력 전압은 어떻게 될까요?
다양한 벡터의 평균과 변조 지수를 사용하기 때문에 회로도만 보고는 인버터 단자의 사용 가능한 전압을 쉽게 알 수 없습니다.
처음부터 시작하여 어디에 도달하는지 살펴보겠습니다.
정류기가 연결된 그리드 전압:

결과적인 DC 링크 전압(낮은 부하 가정):

대체 공식 DC 링크 전압(3상/6펄스 공급에 대한 평균):

(지금은 첫 번째 것에 집중하고 나중에 마지막 것으로 돌아가겠습니다)
이 전압 레벨을 이용해서 출력 전압을 합성해야 합니다.
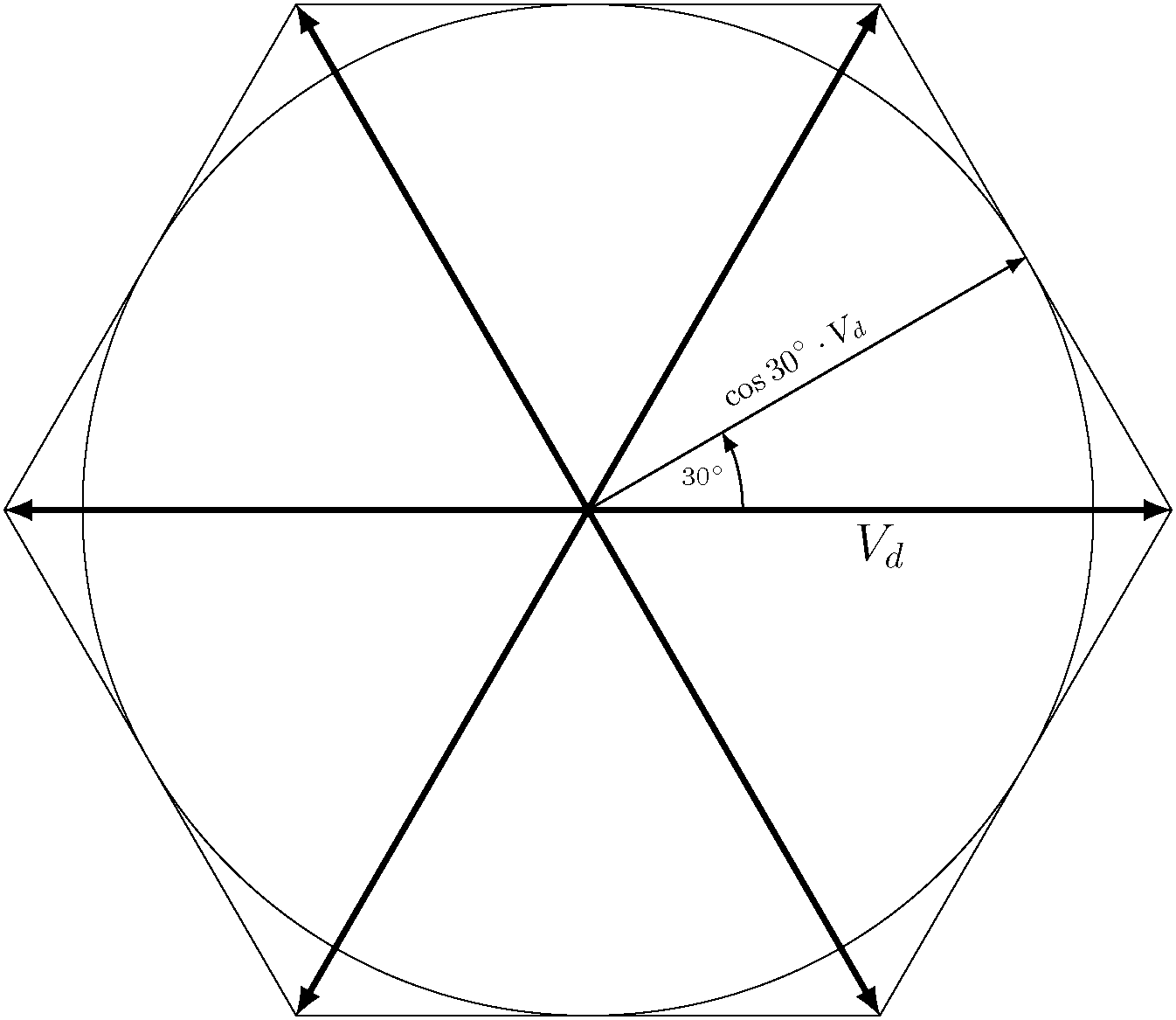
앞서 보여준 것처럼, 여섯 가지 기본 벡터가 있지만, 크기는 아직 명시되지 않았습니다. 각도만 명시되었습니다. 그럼, 다음과 같습니다.

어려웠나요?
위의 정보를 통해 6가지 기본 벡터의 업데이트된 그림을 제시할 수 있습니다. 각 벡터 팁 사이에 선을 그리면 잘 알려진 공간 벡터 육각형이 형성됩니다. 문헌에서 공간 벡터 육각형에 대해 다른 표기법이 사용된다는 점에 유의하세요. 위상 전압, 선 전압, RMS 전압, 일부는 과변조도 포함합니다(이것에 대해서는 나중에 설명하겠습니다. 걱정하지 마세요).
관찰력이 뛰어나신 분은 육각형 내부에 위치한 원을 알아차릴 수 있습니다. 그 반지름은 육각형 경계에서 허용되는 최대 크기로 주어집니다. 이 반지름은 다음과 같습니다.30∘이는 두 인접한 기본 벡터 사이에 정확히 해당합니다.
그러면 최대 RMS 출력 전압은 다음과 같습니다.
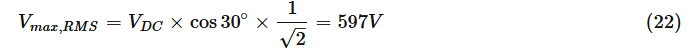
이는 입력 전압보다 낮지만, 육각형을 살펴보면 그 이유가 분명해집니다. 인접한 기본 벡터를 번갈아 가며 변환할 때 평균을 구하고 그 과정에서 일부 전압이 "손실"되기 때문입니다.
이 낮은 전압은 어떤 사람들에게는 약간 실망스러울 수 있습니다. 그리드 전압이 690V일 때, 그에 맞는 690V 모터를 구매하고 싶을 것입니다.
이제 우리는 무엇을 해야 할까?
6. 한 섹터 안에서의 표현
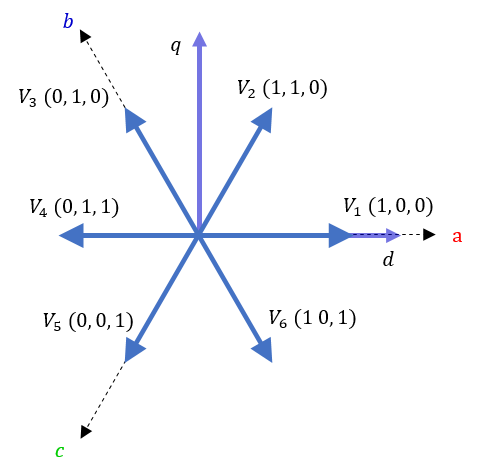
아래 표에서 V1~V6 상태를 유효 전압 벡터 (Active Voltage Vector)라고 하며, DC 전압의 2/3 크기를 가집니다. 그리고 V0와 V7은 영전압 벡터로 부하를 인가하지 않는 상태입니다.

SVPWM의 기본적인 원리는 지령 전압과 인접한 2개의 유효 벡터와 영전압을 이용하여 한 주기 동안 평균적으로 합성하는 것입니다. 이를 식으로 표현하면 식 2 또는 식 3과 같이 나타낼 수 있습니다.
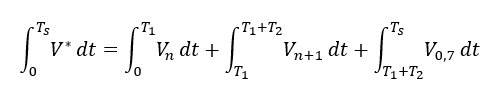



그림. 2 SVPWM의 변조 과정
식 2를 벡터 선도로 표현하면 그림 2와 같이 나타낼 수 있습니다. 전압 지령을 생성하는 과정은 그림 2와 같이 3단계입니다. 이는 스위칭 주파수에 결정된 샘플링 주기마다 반복됩니다. 먼저 0~T1에 해당하는 시간 동안 V1의 방향으로 전압을 인가하면, V1(T1/Ts) 크기의 전압이 발생합니다. 그다음으로 T2 시간 동안 V2 방향으로 전압을 인가하면, 지령 전압과 같은 위상과 크기를 맞출 수 있습니다. 마지막으로 T1과 T2 시간의 합이 샘플링 주기보다 작다면 나머지 시간 (식. 8) 동안에는 영 전압 벡터를 인가합니다. 그림 2와 같이 지령 전압 벡터가 sector I 영역에 위치한 경우 식 4와 같이 표현할 수 있습니다.
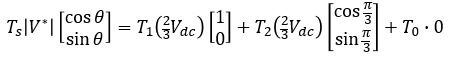
이제 식 4를 통해 유효 전압 벡터 인가 시간을 유도하면 각각 식 5와 식 6과 같이 나타낼 수 있습니다.
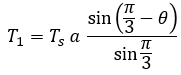
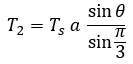
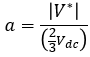
따라서
T1 = k sin ( 60 - Φ ) , T2 = k sin ( Φ ) , k= Ts a / sin(60) ---> C program code 적용
영 전압 벡터 인가 시간은 식 8과 같이 샘플링 주기에서 T1과 T2를 뺀 시간입니다.
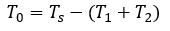
SVPWM에서는 유효 전압 벡터 인가 시간의 합이 샘플링 주기 보다 크면 안 됩니다. 따라서 식 9와 같은 조건으로 표현할 수 있습니다.
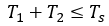
식 5와 식 6을 식 9에 대입하면 식 10과 같이 정리할 수 있습니다.
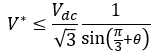
식 10의 의미는 지령 전압 벡터의 범위가 그림 3과 같이 노란색 원 안의 영역에 존재한다는 것입니다. 그림 3의 육각형에 내접하는 원은 선형 변조가 가능한 지령 전압의 영역이기도 합니다.
7. 3차 고조파 주입
안전벨트를 매고 지팡이를 꺼내세요. 이제 우리는 전기공학의 어두운 세계에 발을 들이게 됩니다.
방금 보여준 것처럼, 우리는 우리가 원하는 것에 비해 너무 낮은 출력 전압이라는 문제에 직면해 있습니다. 하지만 우리는 또한 물리적 한계에 직면해 있습니다. 우리는 그것을 구부릴 것입니다. 약간만.
먼저, 아래의 문제를 설명해 보겠습니다.
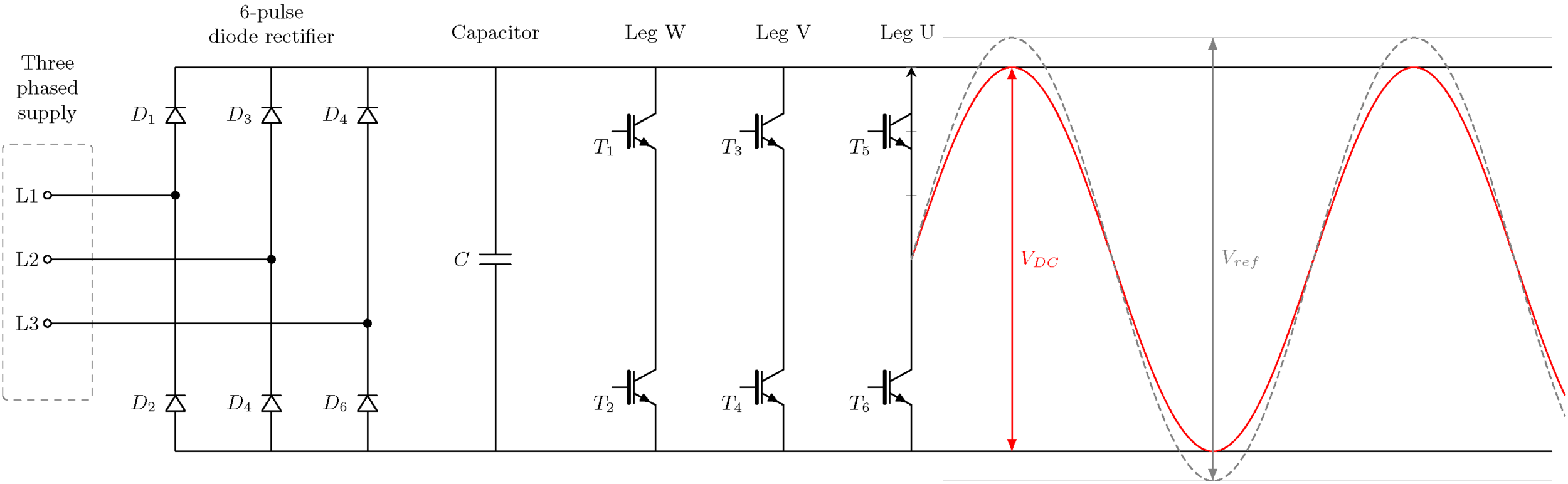
빨간색으로 최대 출력 전압 파형을 표시한 표준 2레벨 인버터. 점선 곡선은 원하는 전압, 즉 입력 rms 전압과 동일한 진폭을 나타냅니다.
DC-링크의 최대 전압 출력은 DC-링크 전압이어야 합니다. 그 위에는 피크 대 피크 전압이 다음과 같은 빨간색 사인파로 표시됩니다.Vdc= 975V. RMS 위상 간 전압은 다음과 같습니다.
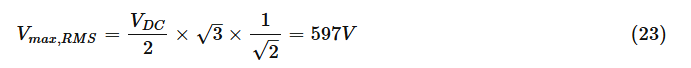
이는 몇 문단에서 언급한 것과 정확히 동일하며, 다른 관점에서 제시한 것입니다. 그리고 우리는 690V에 도달하기 위해 DC 링크 상한을 약 15% 정도 통과 해야 한다는 것을 보여주는 것 외에는 아직 문제를 다루지 않았습니다 . 이것은 불가능해 보일 수 있습니다. 상한은 스위치가 100%의 시간 동안 켜져 있는 스위칭 상태를 나타내는 반면, 하한은 켜진 시간이 0인 상태를 나타냅니다. 그렇다면 스위치가 100% 이상 또는 0% 미만 으로 켜질 수 있는 방법은 무엇입니까 ?
우리가 시도해야 할 기술은 1980년대에 GE에서 일하던 한 엔지니어가 발명한 것으로 (팡파르)라고 불립니다. 제3 고조파 주입이죠.
맞습니다 여러분; 기본 주파수의 3배 주파수를 가진 두 번째 사인파를 추가하면 아래에서 보듯이 매우 우아한 방식으로 문제를 효과적으로 해결할 수 있습니다.
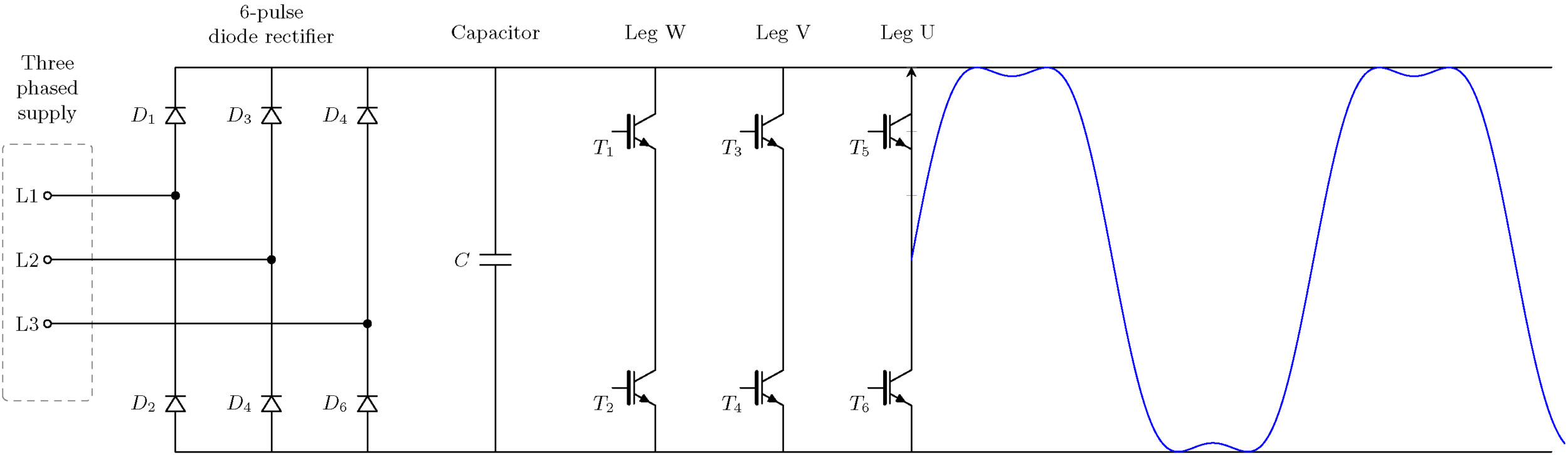
잠깐요, 당신은 말합니까? 어떤 사람들은 부드러운 사인파에 돈을 냈나요?
글쎄요, 요령은 그것이 모두 안에 숨겨져 있다는 것입니다. 위에 있는 파란색 곡선을 구성 사인파로 확장하면(일명 푸리에 확장) 아래 그림 처럼 나타납니다.
이제 그게 더 그럴 듯합니다! 우리는 이제 최대 전압 출력 측면에서 물리적 한계를 성공적으로 우회했고 3차 고조파 주입을 사용하여 모든 것을 깔끔하게 마무리 했습니다.
다음으로 모터가 이것에 대해 어떻게 생각하는지 살펴보겠습니다. 고조파는 거의 항상 원치 않는 현상이므로 결과를 확인해 보겠습니다.
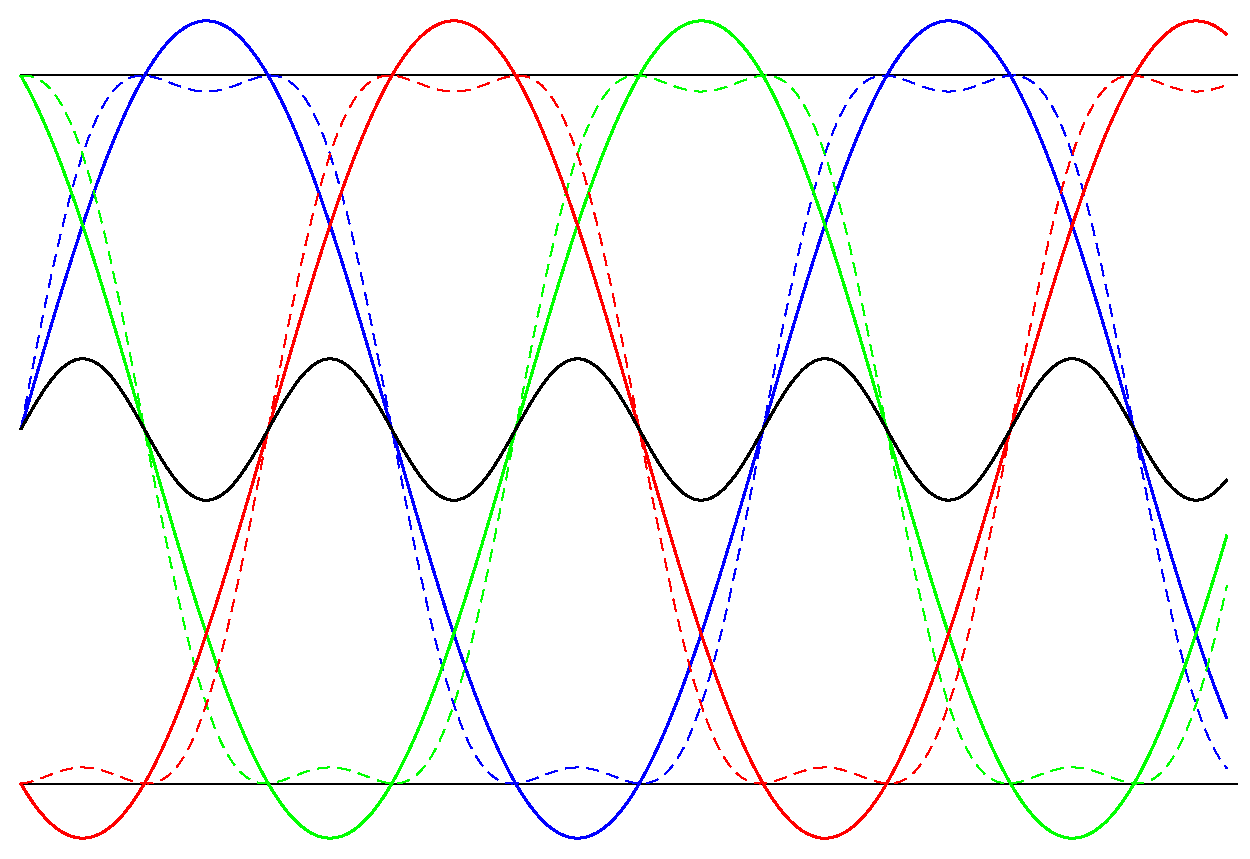
오른쪽 그림은 3상 전압을 모두 3차 고조파 주입을 통해 나타낸 것입니다.
어떤 사람들은 그 곡선에서 이상한 점을 알아차릴 수도 있습니다. 검은색 3차 고조파 곡선은 세 위상 모두에 공통적입니다. 세 위상 모두 중첩되어 있고 완전히 동일하므로 3차 고조파는 이제 공통 모드 파형이 됩니다. 이제 모터 회로의 모든 부분이 DC 링크에 비해 3배의 주파수로 진동합니다.
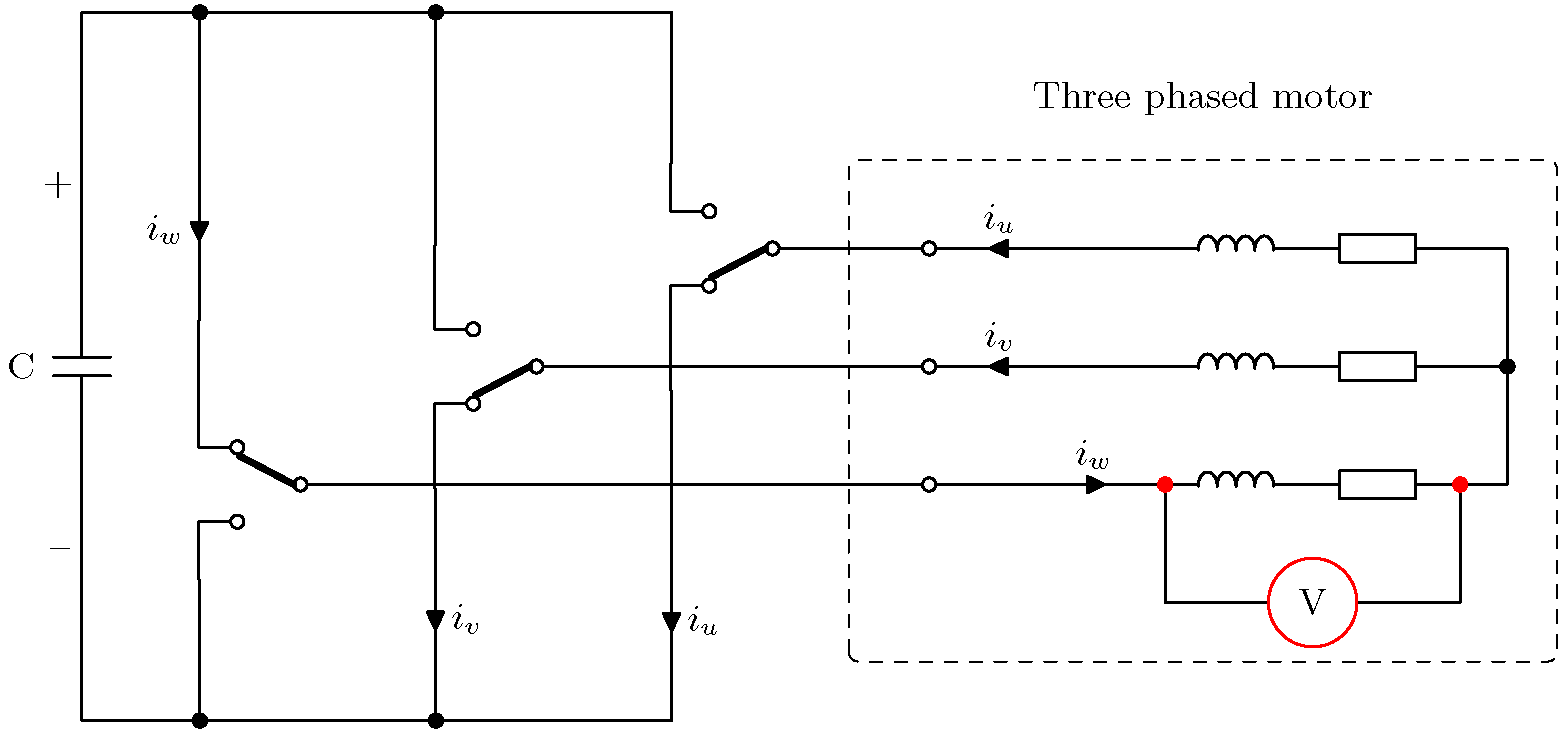
모터의 위상 중성점에 연결된 전압계. 이것은 모터 권선 전압과 3차 고조파가 이에 영향을 미치는지 여부를 보여줍니다.
모터의 중립 지점은 이제 특히 관심의 대상입니다. 이제 질문은 다음과 같습니다.
각 권선의 상-중성선 전압은 얼마입니까?
위상 전압은 큰 사인파와 3차 고조파를 합친 것으로 구성되어 있다는 것을 기억하세요 . 스코프는 이제 위상 전압(그림의 왼쪽 프로브) 에서 중성 전압(오른쪽 프로브)을 뺀 값을 표시합니다.
또한 모터의 모든 지점은 중성점을 포함하여 3차 고조파 주파수와 진폭으로 진동한다는 것을 기억하십시오. 따라서 중성 연결 프로브는 위상 연결 프로브에서 측정할 수 있는 동일한 3차 고조파를 볼 것입니다.
그러면 수학은 다음과 같이 됩니다.
(큰 사인파 + 3차 고조파 사인파) - (3차 고조파 사인파) = (큰 사인파만)
오 예. 3차 고조파 성분 전체가 사라지고 권선은 그것을 알지도 못합니다.
바징가.
8. 변조지수, Modulation index, M
이것은 전압을 스케일링하는 데 사용되는 아주 간단한 요소입니다. 마지막 섹션에서는 3차 고조파 주입을 적용하여 출력 전압을 최대 115.4%까지 스케일링할 수 있다는 것을 보여주었습니다. 즉, 변조 지수는 0에서 1.154까지 범위가 될 수 있습니다.
그러면 출력 위상 간 전압에 대한 공식은 다음과 같습니다.
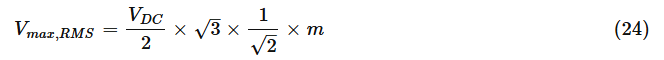
M은 변조지수 인자를 나타냅니다.
아래 애니메이션은 이 개념을 설명합니다.
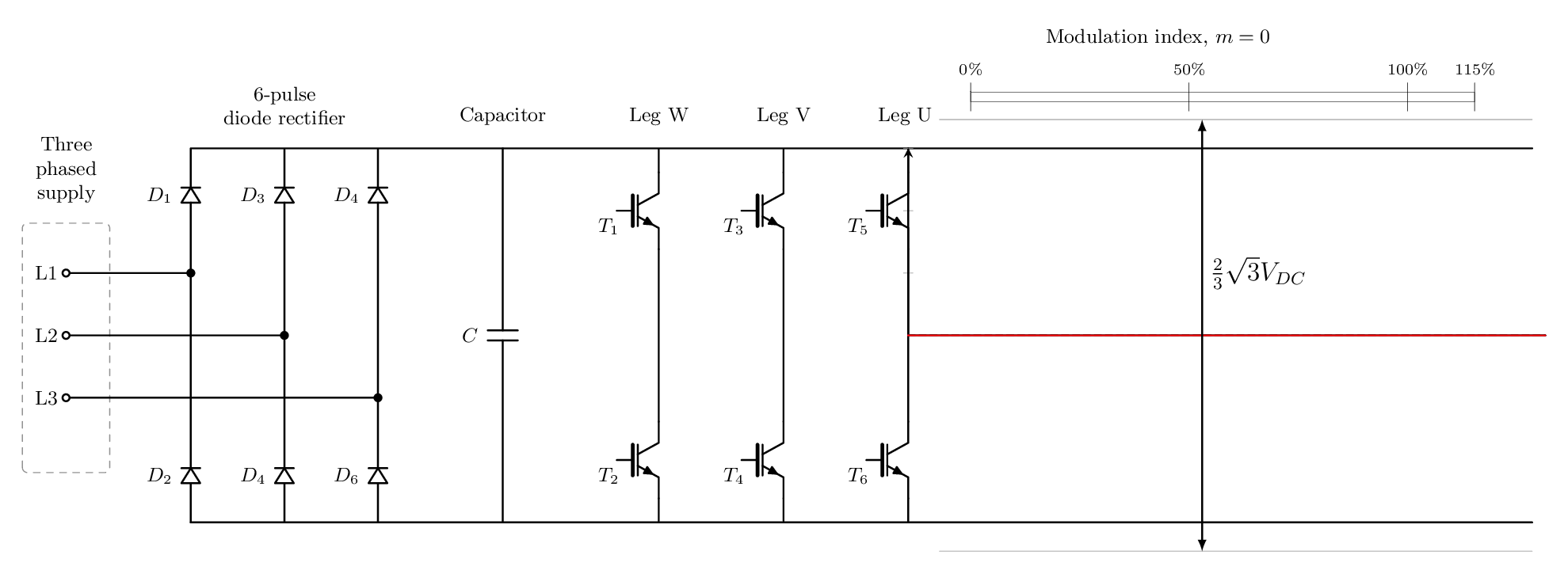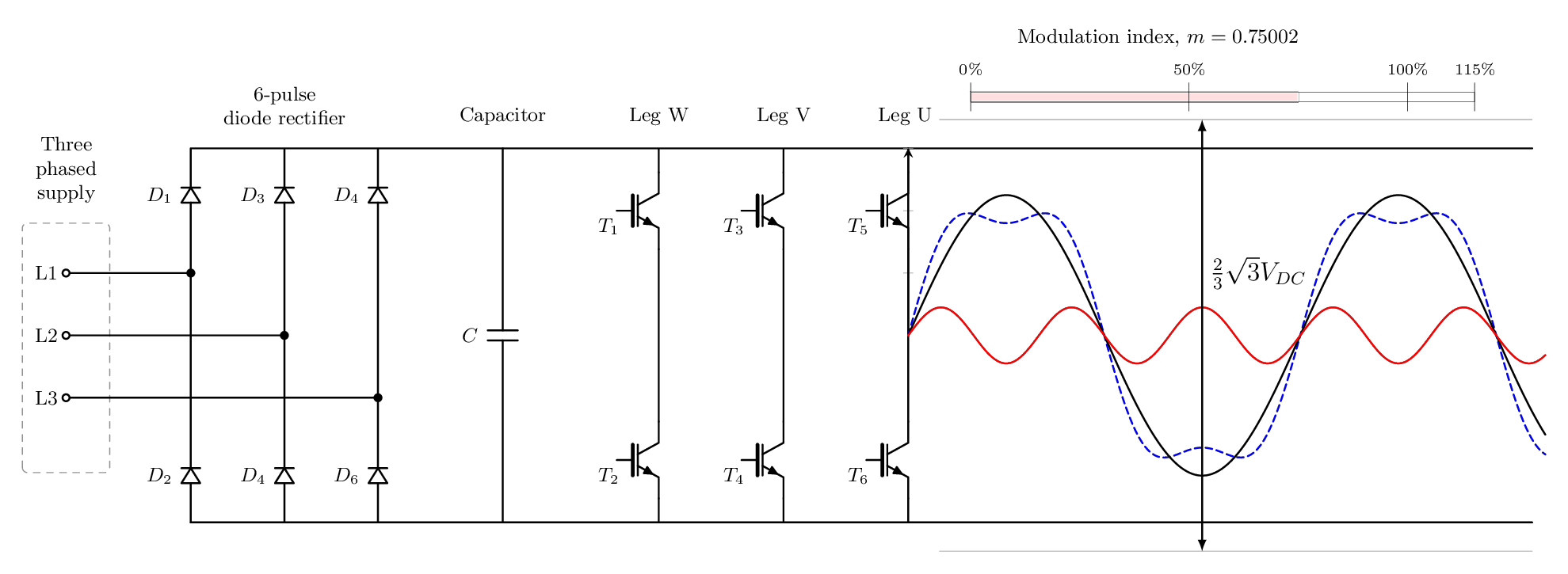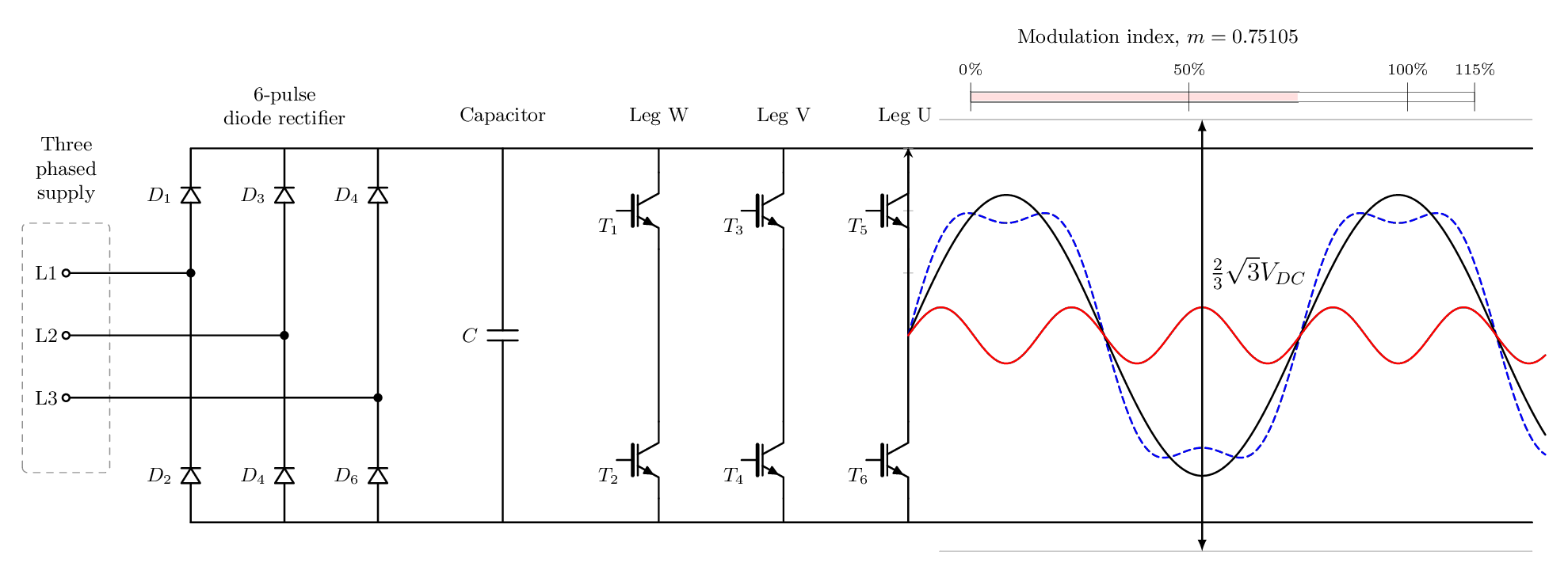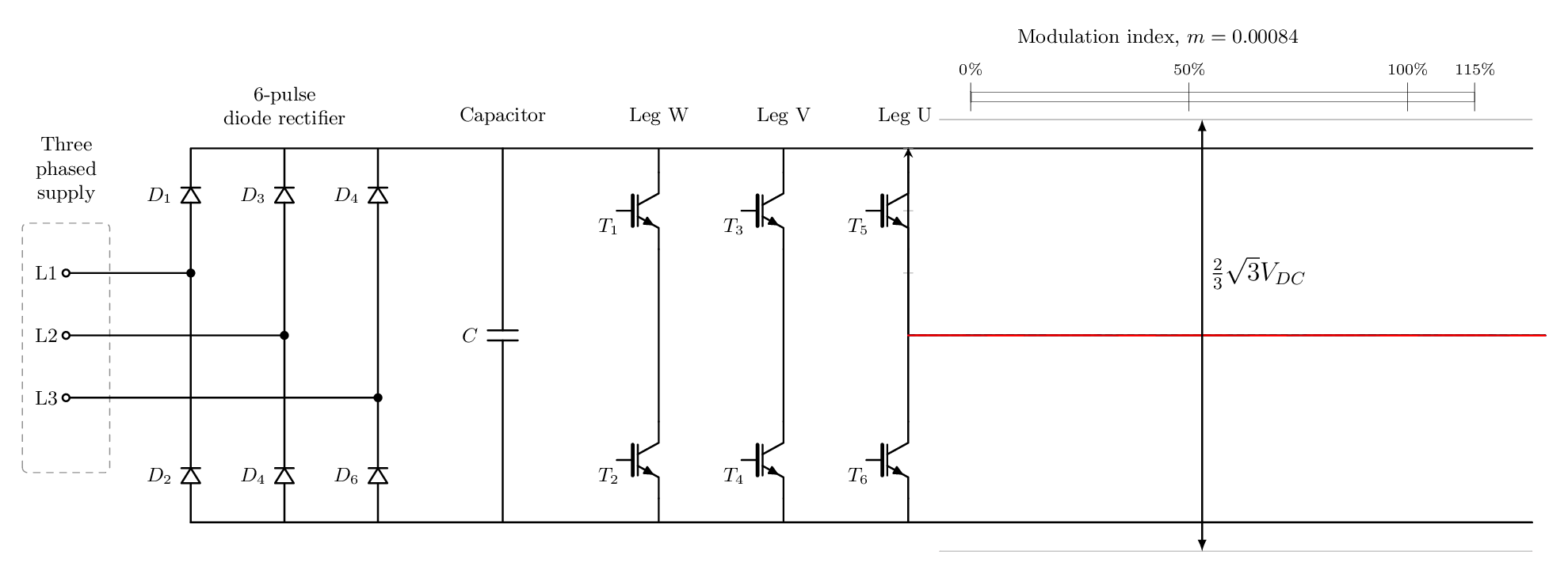
9. 과변조
변조 지수가 1.154를 넘으면 이상한 일이 일어나기 시작합니다. 삼각파와 함께 사용되는 제어 전압은 삼각파 위로 이동합니다 . 이렇게 하면 효과적으로 0 벡터가 제거되고 제어 전압이 얼마나 위로 이동하는지에 따라 각 섹터 내에서 점점 더 긴 기간 동안 다른 제어 전압을 지배하게 됩니다.
인버터는 펄스를 잘라내고 사인파를 점점 더 왜곡(거칠게)하여 6단계 라고 하는 상황이 발생할 때까지 계속합니다. 6단계 작동에서 인버터는 한 번에 하나의 기본 벡터에 머물다가 바로 다음 기본 벡터로 점프한 다음 그 다음 기본 벡터로 점프합니다. 60도 단계와 사각파 작동을 사용하면 모터가 고조파를 많이 생성하고 아마도 정말 끔찍하게 느껴질 것입니다. 다행히도 모터 인덕턴스는 과도한 코깅/토크 리플로 인한 손상을 방지하기 위해 전류를 필터링(평활화)합니다(토크를 생성하는 것은 전압이 아니라 전류라는 것을 기억하세요).
이런 작동 방식은 우리가 처음에 서로 다르고 인접한 기본 벡터의 평균을 구함으로써 피하려고 했던 바로 그 방식입니다.
과변조가 모터 고문처럼 보이지만(실제로 그렇습니다...) 때로는 필요합니다. 지금까지 DC 링크는 항상 다음 계수로 유지된다고 가정했습니다.√2공급 전압보다 높지만 항상 그런 것은 아닙니다.
모터가 최대 속도와 최대 전력으로 작동하는 등 높은 전류가 필요한 경우 그리드에서 소모되는 전류는 상당하므로 정류 다이오드의 작은 DC 저항이 엄청난 전압 강하로 이어집니다(이게 바로 옴의 법칙입니다).
갑자기 DC 링크 전압이 더 이상 975V가 아니라 900V가 되었고, 모터는 정격 값에서 모터 플럭스를 유지하기 위해 최대 속도에서 최대 전압이 필요합니다 . 이 전압에서 1.25의 변조 지수가 필요하며, 이는 보기 흉한 사인파를 생성합니다. 또한 과변조가 더 이상 선형이 아니라는 점에 유의하십시오. 실제로는 자화 곡선의 포화 영역처럼 보이므로 컨트롤러는 원하는(선형화된) 변조 레벨을 달성하기 위해 변조 지수를 증폭해야 합니다.
보기 흉한 사인파로 인해 설계된 3차 고조파 외의 고조파가 나타나기 시작합니다. 이는 로터와 주 권선 모두의 과열과 음향 소음(윙윙거림) 및 토크 리플을 일으킬 수 있습니다. 이는 유도 모터에 적용됩니다. 무브러시 DC 기계는 실제로 이 작동 모드에 맞게 설계되었습니다.
참고
1. 본글은
https://www.switchcraft.org/learning/2017/3/15/space-vector-pwm-intro
공간 벡터 PWM 소개 저자: 잉베 솔바켄(Yngve Solbakken)
을 주로 번역 한 것 입니다.
2.
'개발 > Motor Inverter' 카테고리의 다른 글
| (3상) 모터 제어 Inverter - 방법 비교 pwm, spwm,svpwm,foc (4) | 2025.07.16 |
|---|---|
| (3상) 모터 Inverter - 벡터 제어 - 연재 (1) | 2025.07.15 |
| (3상) 모터 Inverter 종류 - dq 변환 (Clarke + Park 변환) - 연재 (0) | 2025.04.03 |
| (3상) 모터 Inverter 종류 - SPWM, Sinusoidal PWM - 연재 (0) | 2025.04.03 |
| (3상) 모터 Inverter 종류 - 6 Step 인버터 - 연재 (0) | 2025.04.03 |


